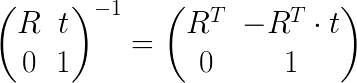This forum is disabled, please visit https://forum.opencv.org
 | 1 | initial version |
If you have the pose for the board(cMboard) and the poses for the two balls (cMball1 and cMball2) (that means that you can reproject the board and the balls models in the image), it should be possible to have the pose for the balls with respect to the board frame as:
 | 2 | No.2 Revision |
If you have the pose for the board(cMboard) board:
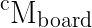
and the poses for the two balls (cMball1 balls:
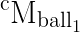 and
and 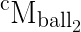 ,
,that means that you can reproject the models of the board and the balls models in the image), image):
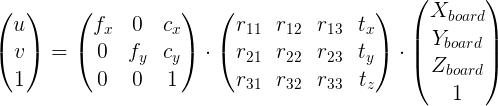 ,
,
it should be possible to have the pose for the balls with respect to the board frame as:
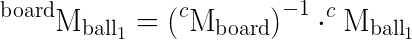
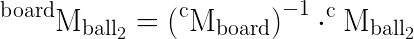 .
.An homogeneous transformation matrix is composed of a rotation part and a translation part:
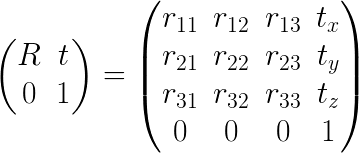
The inverse of an homogeneous matrix can be calculated easily as:
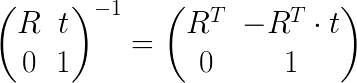
 | 3 | No.3 Revision |
If you have the pose for the board:
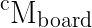
and the poses for the two balls:
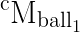 and
and 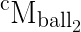 ,
,that means that you can reproject the models of the board and the balls in the image):
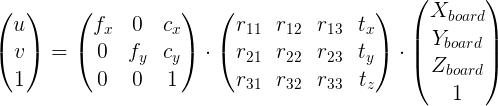 ,
,
it should be possible to have the pose for the balls with respect to the board frame as:
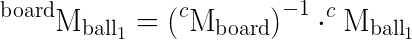
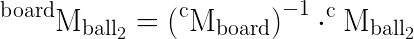 .
.You can transform a 3D coordinate expressed in a specific frame to another frame as for example:
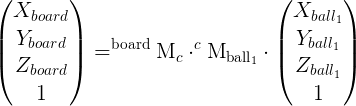
An homogeneous transformation matrix is composed of a rotation part and a translation part:
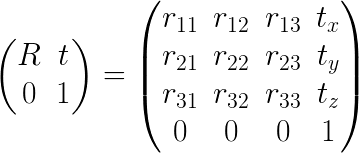
The inverse of an homogeneous matrix can be calculated easily as: