This forum is disabled, please visit https://forum.opencv.org
 | 1 | initial version |
It should be possible if you know:
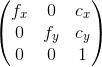
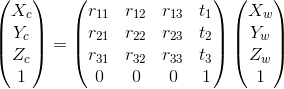
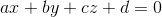
For the plane equation, you should find a way to know the coordinates of 3 points in the world coordinate that lie on the same plane that contains the hole.
Then, you can change their coordinates to the camera frame knowing the camera pose and compute the plane equation.
Convert the 2D image coordinate of the hole in the normalized camera frame:
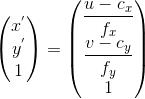
Get the scale factor: 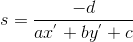
The 3D coordinate of the hole in the camera frame is then: 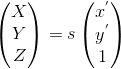
Different formulas:
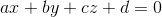
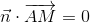
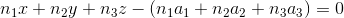
You can then identify the quadruplet 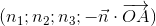 with the quadruplet
with the quadruplet 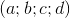 .
.
We can have a first plane that contains the hole and another plane parallel to the first but which passes by a point at a normalized coordinate z=1 (obtained from the 2d coordinate): 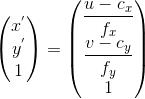 .
.
For the two plane equations, the coefficients a, b, c are the same, only the coefficient d is different.
The "scale factor" is then:
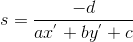
 | 2 | No.2 Revision |
It should be possible if you know:
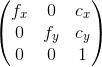
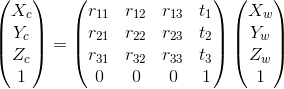
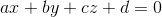
For the plane equation, you should find a way to know the coordinates of 3 points in the world coordinate that lie on the same plane that contains the hole.
Then, you can change their coordinates to the camera frame knowing the camera pose and compute the plane equation.
Convert the 2D image coordinate of the hole in the normalized camera frame:
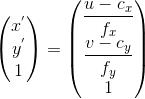
Get the scale factor: 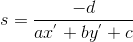
The 3D coordinate of the hole in the camera frame is then: 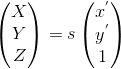
Different formulas:
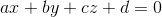
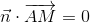
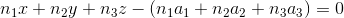
You can then identify the quadruplet 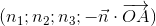 with the quadruplet
with the quadruplet 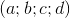 .
.
We can have a first plane that contains the hole and another plane parallel to the first but which passes by a point at a normalized coordinate z=1 (obtained from the 2d coordinate): 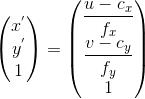 .
.
For the two plane equations, the coefficients a, b, c are the same, only the coefficient d is different.
The "scale factor" is then:
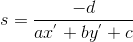
Edit: Your case is a little easier as the camera is almost parallel to the surface. You could use the hole diameter to compute the "scale factor" knowing the ratio between the hole diameter in the real world and the hole diameter in pixel after a calibration step.
 | 3 | No.3 Revision |
It should be possible if you know:
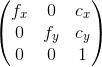
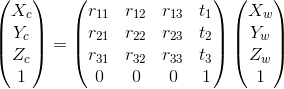
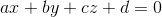
For the plane equation, you should find a way to know the coordinates of 3 points in the world coordinate that lie on the same plane that contains the hole.
Then, you can change their coordinates to the camera frame knowing the camera pose and compute the plane equation.
Convert the 2D image coordinate of the hole in the normalized camera frame:
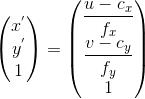
Get the scale factor: 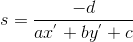
The 3D coordinate of the hole in the camera frame is then: 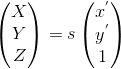
Different formulas:
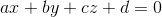
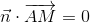
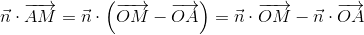
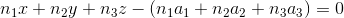
You can then identify the quadruplet 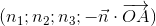 with the quadruplet
with the quadruplet 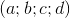 .
.
We can have a first plane that contains the hole and another plane parallel to the first but which passes by a point at a normalized coordinate z=1 (obtained from the 2d coordinate): 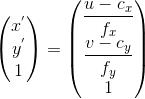 .
.
For the two plane equations, the coefficients a, b, c are the same, only the coefficient d is different.
The "scale factor" is then:
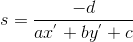
Edit: Your case is a little easier as the camera is almost parallel to the surface. You could use the hole diameter to compute the "scale factor" knowing the ratio between the hole diameter in the real world and the hole diameter in pixel after a calibration step.
 | 4 | No.4 Revision |
It should be possible if you know:
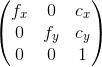
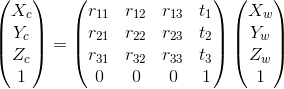
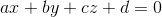
For the plane equation, you should find a way to know the coordinates of 3 points in the world coordinate that lie on the same plane that contains the hole.
Then, you can change their coordinates to the camera frame knowing the camera pose and compute the plane equation.
Convert the 2D image coordinate of the hole in the normalized camera frame:
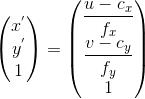
Get the scale factor: 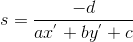
The 3D coordinate of the hole in the camera frame is then: 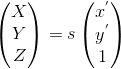
Different formulas:
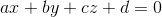
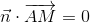
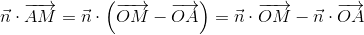
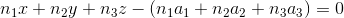
You can then identify the quadruplet 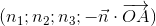 with the quadruplet
with the quadruplet 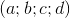 .
.
We can have a first plane that contains the hole and another plane parallel to the first but which passes by a point at a normalized coordinate z=1 (obtained from the 2d coordinate): 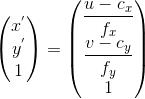 .
.
For the two plane equations, the coefficients a, b, c are the same, only the coefficient d is different.
The "scale factor" is then:
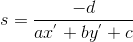
Edit: Your case is a little easier as the camera is almost parallel to the surface. You could use the hole diameter to compute the "scale factor" knowing the ratio between the hole diameter in the real world and the hole diameter in pixel after a calibration step.
Edit2 (2016/11/27):
Here a full working example. The data used to estimate the camera intrinsic matrix can be found in the OpenCV sample data directory (I used the left images).
The example code is a little bit long. What it does:
cv::findChessboardCorners (image used is left04.jpg)cv::solvePnPCode:
#include <iostream>
#include <opencv2/opencv.hpp>
//@ref: http://answers.opencv.org/question/67008/can-i-get-2d-world-coordinates-from-a-single-image-uv-coords/
enum Pattern { CHESSBOARD, CIRCLES_GRID, ASYMMETRIC_CIRCLES_GRID };
static void calcChessboardCorners(cv::Size boardSize, float squareSize, std::vector<cv::Point3f>& corners, Pattern patternType = CHESSBOARD) {
corners.resize(0);
switch(patternType) {
case CHESSBOARD:
case CIRCLES_GRID:
for( int i = 0; i < boardSize.height; i++ )
for( int j = 0; j < boardSize.width; j++ )
corners.push_back(cv::Point3f(float(j*squareSize),
float(i*squareSize), 0));
break;
case ASYMMETRIC_CIRCLES_GRID:
for( int i = 0; i < boardSize.height; i++ )
for( int j = 0; j < boardSize.width; j++ )
corners.push_back(cv::Point3f(float((2*j + i % 2)*squareSize),
float(i*squareSize), 0));
break;
default:
CV_Error(cv::Error::StsBadArg, "Unknown pattern type\n");
}
}
double checkCameraPose(const std::vector<cv::Point3f> &modelPts, const std::vector<cv::Point2f> &imagePts, const cv::Mat &cameraMatrix,
const cv::Mat &distCoeffs, const cv::Mat &rvec, const cv::Mat &tvec) {
std::vector<cv::Point2f> projectedPts;
cv::projectPoints(modelPts, rvec, tvec, cameraMatrix, distCoeffs, projectedPts);
double rms = 0.0;
for (size_t i = 0; i < projectedPts.size(); i++) {
rms += (projectedPts[i].x-imagePts[i].x)*(projectedPts[i].x-imagePts[i].x) + (projectedPts[i].y-imagePts[i].y)*(projectedPts[i].y-imagePts[i].y);
}
return sqrt(rms / projectedPts.size());
}
cv::Point3f transformPoint(const cv::Point3f &pt, const cv::Mat &rvec, const cv::Mat &tvec) {
//Compute res = (R | T) . pt
cv::Mat rotationMatrix;
cv::Rodrigues(rvec, rotationMatrix);
cv::Mat transformationMatrix = (cv::Mat_<double>(4, 4) << rotationMatrix.at<double>(0,0), rotationMatrix.at<double>(0,1), rotationMatrix.at<double>(0,2), tvec.at<double>(0),
rotationMatrix.at<double>(1,0), rotationMatrix.at<double>(1,1), rotationMatrix.at<double>(1,2), tvec.at<double>(1),
rotationMatrix.at<double>(2,0), rotationMatrix.at<double>(2,1), rotationMatrix.at<double>(2,2), tvec.at<double>(2),
0, 0, 0, 1);
cv::Mat homogeneousPt = (cv::Mat_<double>(4, 1) << pt.x, pt.y, pt.z, 1.0);
cv::Mat transformedPtMat = transformationMatrix * homogeneousPt;
cv::Point3f transformedPt(transformedPtMat.at<double>(0), transformedPtMat.at<double>(1), transformedPtMat.at<double>(2));
return transformedPt;
}
cv::Point3f transformPointInverse(const cv::Point3f &pt, const cv::Mat &rvec, const cv::Mat &tvec) {
//Compute res = (R^t | -R^t . T) . pt
cv::Mat rotationMatrix;
cv::Rodrigues(rvec, rotationMatrix);
rotationMatrix = rotationMatrix.t();
cv::Mat translation = -rotationMatrix*tvec;
cv::Mat transformationMatrix = (cv::Mat_<double>(4, 4) << rotationMatrix.at<double>(0,0), rotationMatrix.at<double>(0,1), rotationMatrix.at<double>(0,2), translation.at<double>(0),
rotationMatrix.at<double>(1,0), rotationMatrix.at<double>(1,1), rotationMatrix.at<double>(1,2), translation.at<double>(1),
rotationMatrix.at<double>(2,0), rotationMatrix.at<double>(2,1), rotationMatrix.at<double>(2,2), translation.at<double>(2),
0, 0, 0, 1);
cv::Mat homogeneousPt = (cv::Mat_<double>(4, 1) << pt.x, pt.y, pt.z, 1.0);
cv::Mat transformedPtMat = transformationMatrix * homogeneousPt;
cv::Point3f transformedPt(transformedPtMat.at<double>(0), transformedPtMat.at<double>(1), transformedPtMat.at<double>(2));
return transformedPt;
}
void computePlaneEquation(const cv::Point3f &p0, const cv::Point3f &p1, const cv::Point3f &p2, float &a, float &b, float &c, float &d) {
//Vector p0_p1
cv::Point3f p0_p1;
p0_p1.x = p0.x - p1.x;
p0_p1.y = p0.y - p1.y;
p0_p1.z = p0.z - p1.z;
//Vector p0_p2
cv::Point3f p0_p2;
p0_p2.x = p0.x - p2.x;
p0_p2.y = p0.y - p2.y;
p0_p2.z = p0.z - p2.z;
//Normal vector
cv::Point3f n = p0_p1.cross(p0_p2);
a = n.x;
b = n.y;
c = n.z;
d = -(a*p0.x + b*p0.y + c*p0.z);
float norm = sqrt(a*a + b*b + c*c);
a /= norm;
b /= norm;
c /= norm;
d /= norm;
}
cv::Point3f compute3DOnPlaneFrom2D(const cv::Point2f &imagePt, const cv::Mat &cameraMatrix, const float a, const float b, const float c, const float d) {
double fx = cameraMatrix.at<double>(0,0);
double fy = cameraMatrix.at<double>(1,1);
double cx = cameraMatrix.at<double>(0,2);
double cy = cameraMatrix.at<double>(1,2);
cv::Point2f normalizedImagePt;
normalizedImagePt.x = (imagePt.x - cx) / fx;
normalizedImagePt.y = (imagePt.y - cy) / fy;
float s = -d / (a*normalizedImagePt.x + b*normalizedImagePt.y + c);
cv::Point3f pt;
pt.x = s*normalizedImagePt.x;
pt.y = s*normalizedImagePt.y;
pt.z = s;
return pt;
}
int main() {
cv::Mat img = cv::imread("data/left04.jpg", cv::IMREAD_GRAYSCALE);
cv::Mat view;
cv::cvtColor(img, view, cv::COLOR_GRAY2BGR);
cv::Size boardSize(9, 6);
std::vector<cv::Point2f> pointbuf;
bool found = cv::findChessboardCorners( img, boardSize, pointbuf, cv::CALIB_CB_ADAPTIVE_THRESH | cv::CALIB_CB_FAST_CHECK | cv::CALIB_CB_NORMALIZE_IMAGE);
if(found) {
cv::drawChessboardCorners( view, boardSize, cv::Mat(pointbuf), found );
} else {
return -1;
}
cv::imshow("Image", view);
cv::waitKey();
//Compute chessboard model points
std::vector<cv::Point3f> modelPts;
float squareSize = 1.0f;
calcChessboardCorners(boardSize, squareSize, modelPts);
//Intrinsic
cv::Mat cameraMatrix = (cv::Mat_<double>(3, 3) << 5.3590117051349637e+02, 0, 3.4227429926016583e+02,
0, 5.3590117051349637e+02, 2.3557560607943688e+02,
0, 0, 1);
cv::Mat distCoeffs = (cv::Mat_<double>(5, 1) << -2.6643160989580222e-01, -3.8505305722612772e-02, 1.7844280073183410e-03,
-2.7702634246810361e-04, 2.3850218962079497e-01);
//Compute camera pose
cv::Mat rvec, tvec;
cv::solvePnP(modelPts, pointbuf, cameraMatrix, distCoeffs, rvec, tvec);
//Check camera pose
double rms = checkCameraPose(modelPts, pointbuf, cameraMatrix, distCoeffs, rvec, tvec);
std::cout << "RMS error for camera pose=" << rms << std::endl;
//Transform model point (in object frame) to the camera frame
cv::Point3f pt0 = transformPoint(modelPts[0], rvec, tvec);
cv::Point3f pt1 = transformPoint(modelPts[8], rvec, tvec);
cv::Point3f pt2 = transformPoint(modelPts[53], rvec, tvec);
//Compute plane equation in the camera frame
float a, b, c, d;
computePlaneEquation(pt0, pt1, pt2, a, b, c, d);
std::cout << "Plane equation=" << a << " ; " << b << " ; " << c << " ; " << d << std::endl;
//Compute 3D from 2D
std::vector<cv::Point3f> pts3dCameraFrame, pts3dObjectFrame;
double rms_3D = 0.0;
for (size_t i = 0; i < pointbuf.size(); i++) {
cv::Point3f pt = compute3DOnPlaneFrom2D(pointbuf[i], cameraMatrix, a, b, c, d);
pts3dCameraFrame.push_back(pt);
cv::Point3f ptObjectFrame = transformPointInverse(pt, rvec, tvec);
pts3dObjectFrame.push_back(ptObjectFrame);
rms_3D += (modelPts[i].x-ptObjectFrame.x)*(modelPts[i].x-ptObjectFrame.x) + (modelPts[i].y-ptObjectFrame.y)*(modelPts[i].y-ptObjectFrame.y) +
(modelPts[i].z-ptObjectFrame.z)*(modelPts[i].z-ptObjectFrame.z);
std::cout << "modelPts[" << i << "]=" << modelPts[i] << " ; calc=" << ptObjectFrame << std::endl;
}
std::cout << "RMS error for model points=" << sqrt(rms_3D / pointbuf.size()) << std::endl;
return 0;
}
 | 5 | No.5 Revision |
It should be possible if you know:
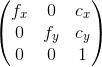
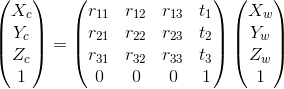
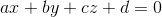
For the plane equation, you should find a way to know the coordinates of 3 points in the world coordinate that lie on the same plane that contains the hole.
Then, you can change their coordinates to the camera frame knowing the camera pose and compute the plane equation.
Convert the 2D image coordinate of the hole in the normalized camera frame:
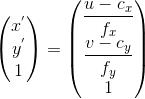
Get the scale factor: 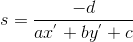
The 3D coordinate of the hole in the camera frame is then: 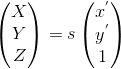
Different formulas:
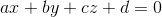
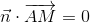
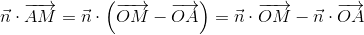
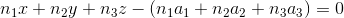
You can then identify the quadruplet 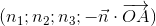 with the quadruplet
with the quadruplet 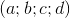 .
.
We can have a first plane that contains the hole and another plane parallel to the first but which passes by a point at a normalized coordinate z=1 (obtained from the 2d coordinate): 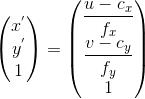 .
.
For the two plane equations, the coefficients a, b, c are the same, only the coefficient d is different.
The "scale factor" is then:
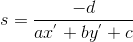
Edit: Your case is a little easier as the camera is almost parallel to the surface. You could use the hole diameter to compute the "scale factor" knowing the ratio between the hole diameter in the real world and the hole diameter in pixel after a calibration step.
Edit2 (2016/11/27):
Here a full working example. The data used to estimate the camera intrinsic matrix can be found in the OpenCV sample data directory (I used the left images).
The example code is a little bit long. What it does:
cv::findChessboardCorners (image used is left04.jpg)cv::solvePnPCode:
#include <iostream>
#include <opencv2/opencv.hpp>
//@ref: http://answers.opencv.org/question/67008/can-i-get-2d-world-coordinates-from-a-single-image-uv-coords/
enum Pattern { CHESSBOARD, CIRCLES_GRID, ASYMMETRIC_CIRCLES_GRID };
static void calcChessboardCorners(cv::Size boardSize, float squareSize, std::vector<cv::Point3f>& corners, Pattern patternType = CHESSBOARD) {
corners.resize(0);
switch(patternType) {
case CHESSBOARD:
case CIRCLES_GRID:
for( int i = 0; i < boardSize.height; i++ )
for( int j = 0; j < boardSize.width; j++ )
corners.push_back(cv::Point3f(float(j*squareSize),
float(i*squareSize), 0));
break;
case ASYMMETRIC_CIRCLES_GRID:
for( int i = 0; i < boardSize.height; i++ )
for( int j = 0; j < boardSize.width; j++ )
corners.push_back(cv::Point3f(float((2*j + i % 2)*squareSize),
float(i*squareSize), 0));
break;
default:
CV_Error(cv::Error::StsBadArg, "Unknown pattern type\n");
}
}
double checkCameraPose(const std::vector<cv::Point3f> &modelPts, const std::vector<cv::Point2f> &imagePts, const cv::Mat &cameraMatrix,
const cv::Mat &distCoeffs, const cv::Mat &rvec, const cv::Mat &tvec) {
std::vector<cv::Point2f> projectedPts;
cv::projectPoints(modelPts, rvec, tvec, cameraMatrix, distCoeffs, projectedPts);
double rms = 0.0;
for (size_t i = 0; i < projectedPts.size(); i++) {
rms += (projectedPts[i].x-imagePts[i].x)*(projectedPts[i].x-imagePts[i].x) + (projectedPts[i].y-imagePts[i].y)*(projectedPts[i].y-imagePts[i].y);
}
return sqrt(rms / projectedPts.size());
}
cv::Point3f transformPoint(const cv::Point3f &pt, const cv::Mat &rvec, const cv::Mat &tvec) {
//Compute res = (R | T) . pt
cv::Mat rotationMatrix;
cv::Rodrigues(rvec, rotationMatrix);
cv::Mat transformationMatrix = (cv::Mat_<double>(4, 4) << rotationMatrix.at<double>(0,0), rotationMatrix.at<double>(0,1), rotationMatrix.at<double>(0,2), tvec.at<double>(0),
rotationMatrix.at<double>(1,0), rotationMatrix.at<double>(1,1), rotationMatrix.at<double>(1,2), tvec.at<double>(1),
rotationMatrix.at<double>(2,0), rotationMatrix.at<double>(2,1), rotationMatrix.at<double>(2,2), tvec.at<double>(2),
0, 0, 0, 1);
cv::Mat homogeneousPt = (cv::Mat_<double>(4, 1) << pt.x, pt.y, pt.z, 1.0);
cv::Mat transformedPtMat = transformationMatrix * homogeneousPt;
cv::Point3f transformedPt(transformedPtMat.at<double>(0), transformedPtMat.at<double>(1), transformedPtMat.at<double>(2));
return transformedPt;
}
cv::Point3f transformPointInverse(const cv::Point3f &pt, const cv::Mat &rvec, const cv::Mat &tvec) {
//Compute res = (R^t | -R^t . T) . pt
cv::Mat rotationMatrix;
cv::Rodrigues(rvec, rotationMatrix);
rotationMatrix = rotationMatrix.t();
cv::Mat translation = -rotationMatrix*tvec;
cv::Mat transformationMatrix = (cv::Mat_<double>(4, 4) << rotationMatrix.at<double>(0,0), rotationMatrix.at<double>(0,1), rotationMatrix.at<double>(0,2), translation.at<double>(0),
rotationMatrix.at<double>(1,0), rotationMatrix.at<double>(1,1), rotationMatrix.at<double>(1,2), translation.at<double>(1),
rotationMatrix.at<double>(2,0), rotationMatrix.at<double>(2,1), rotationMatrix.at<double>(2,2), translation.at<double>(2),
0, 0, 0, 1);
cv::Mat homogeneousPt = (cv::Mat_<double>(4, 1) << pt.x, pt.y, pt.z, 1.0);
cv::Mat transformedPtMat = transformationMatrix * homogeneousPt;
cv::Point3f transformedPt(transformedPtMat.at<double>(0), transformedPtMat.at<double>(1), transformedPtMat.at<double>(2));
return transformedPt;
}
void computePlaneEquation(const cv::Point3f &p0, const cv::Point3f &p1, const cv::Point3f &p2, float &a, float &b, float &c, float &d) {
//Vector p0_p1
cv::Point3f p0_p1;
p0_p1.x = p0.x - p1.x;
p0_p1.y = p0.y - p1.y;
p0_p1.z = p0.z - p1.z;
//Vector p0_p2
cv::Point3f p0_p2;
p0_p2.x = p0.x - p2.x;
p0_p2.y = p0.y - p2.y;
p0_p2.z = p0.z - p2.z;
//Normal vector
cv::Point3f n = p0_p1.cross(p0_p2);
a = n.x;
b = n.y;
c = n.z;
d = -(a*p0.x + b*p0.y + c*p0.z);
float norm = sqrt(a*a + b*b + c*c);
a /= norm;
b /= norm;
c /= norm;
d /= norm;
}
cv::Point3f compute3DOnPlaneFrom2D(const cv::Point2f &imagePt, const cv::Mat &cameraMatrix, const float a, const float b, const float c, const float d) {
double fx = cameraMatrix.at<double>(0,0);
double fy = cameraMatrix.at<double>(1,1);
double cx = cameraMatrix.at<double>(0,2);
double cy = cameraMatrix.at<double>(1,2);
cv::Point2f normalizedImagePt;
normalizedImagePt.x = (imagePt.x - cx) / fx;
normalizedImagePt.y = (imagePt.y - cy) / fy;
float s = -d / (a*normalizedImagePt.x + b*normalizedImagePt.y + c);
cv::Point3f pt;
pt.x = s*normalizedImagePt.x;
pt.y = s*normalizedImagePt.y;
pt.z = s;
return pt;
}
int main() {
cv::Mat img = cv::imread("data/left04.jpg", cv::IMREAD_GRAYSCALE);
cv::Mat view;
cv::cvtColor(img, view, cv::COLOR_GRAY2BGR);
cv::Size boardSize(9, 6);
std::vector<cv::Point2f> pointbuf;
bool found = cv::findChessboardCorners( img, boardSize, pointbuf, cv::CALIB_CB_ADAPTIVE_THRESH | cv::CALIB_CB_FAST_CHECK | cv::CALIB_CB_NORMALIZE_IMAGE);
if(found) {
cv::drawChessboardCorners( view, boardSize, cv::Mat(pointbuf), found );
} else {
return -1;
}
cv::imshow("Image", view);
cv::waitKey();
//Compute chessboard model points
std::vector<cv::Point3f> modelPts;
float squareSize = 1.0f;
calcChessboardCorners(boardSize, squareSize, modelPts);
//Intrinsic
cv::Mat cameraMatrix = (cv::Mat_<double>(3, 3) << 5.3590117051349637e+02, 0, 3.4227429926016583e+02,
0, 5.3590117051349637e+02, 2.3557560607943688e+02,
0, 0, 1);
cv::Mat distCoeffs = (cv::Mat_<double>(5, 1) << -2.6643160989580222e-01, -3.8505305722612772e-02, 1.7844280073183410e-03,
-2.7702634246810361e-04, 2.3850218962079497e-01);
//Compute camera pose
cv::Mat rvec, tvec;
cv::solvePnP(modelPts, pointbuf, cameraMatrix, distCoeffs, rvec, tvec);
//Check camera pose
double rms = checkCameraPose(modelPts, pointbuf, cameraMatrix, distCoeffs, rvec, tvec);
std::cout << "RMS error for camera pose=" << rms << std::endl;
//Transform model point (in object frame) to the camera frame
cv::Point3f pt0 = transformPoint(modelPts[0], rvec, tvec);
cv::Point3f pt1 = transformPoint(modelPts[8], rvec, tvec);
cv::Point3f pt2 = transformPoint(modelPts[53], rvec, tvec);
//Compute plane equation in the camera frame
float a, b, c, d;
computePlaneEquation(pt0, pt1, pt2, a, b, c, d);
std::cout << "Plane equation=" << a << " ; " << b << " ; " << c << " ; " << d << std::endl;
//Compute 3D from 2D
std::vector<cv::Point3f> pts3dCameraFrame, pts3dObjectFrame;
double rms_3D = 0.0;
for (size_t i = 0; i < pointbuf.size(); i++) {
cv::Point3f pt = compute3DOnPlaneFrom2D(pointbuf[i], cameraMatrix, a, b, c, d);
pts3dCameraFrame.push_back(pt);
cv::Point3f ptObjectFrame = transformPointInverse(pt, rvec, tvec);
pts3dObjectFrame.push_back(ptObjectFrame);
rms_3D += (modelPts[i].x-ptObjectFrame.x)*(modelPts[i].x-ptObjectFrame.x) + (modelPts[i].y-ptObjectFrame.y)*(modelPts[i].y-ptObjectFrame.y) +
(modelPts[i].z-ptObjectFrame.z)*(modelPts[i].z-ptObjectFrame.z);
std::cout << "modelPts[" << i << "]=" << modelPts[i] << " ; calc=" << ptObjectFrame << std::endl;
}
std::cout << "RMS error for model points=" << sqrt(rms_3D / pointbuf.size()) << std::endl;
return 0;
}
 | 6 | No.6 Revision |
It should be possible if you know:
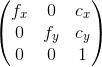
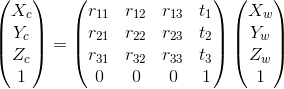
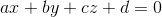
For the plane equation, you should find a way to know the coordinates of 3 points in the world coordinate that lie on the same plane that contains the hole.
Then, you can change their coordinates to the camera frame knowing the camera pose and compute the plane equation.
Convert the 2D image coordinate of the hole in the normalized camera frame:
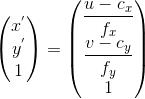
Get the scale factor: 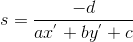
The 3D coordinate of the hole in the camera frame is then: 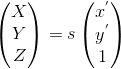
Different formulas:
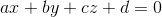
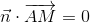
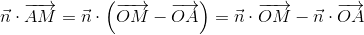
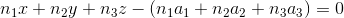
You can then identify the quadruplet 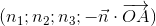 with the quadruplet
with the quadruplet 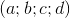 .
.
We can have a first plane that contains the hole and another plane parallel to the first but which passes by a point at a normalized coordinate z=1 (obtained from the 2d coordinate): 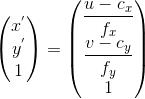 .
.
For the two plane equations, the coefficients a, b, c are the same, only the coefficient d is different.
The "scale factor" is then:
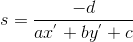
Edit: Your case is a little easier as the camera is almost parallel to the surface. You could use the hole diameter to compute the "scale factor" knowing the ratio between the hole diameter in the real world and the hole diameter in pixel after a calibration step.
Edit2 (2016/11/27):
Here a full working example. The data used to estimate the camera intrinsic matrix can be found in the OpenCV sample data directory (I used the left images).images). Should also be possible to do the same by computing the point from the intersection between the image ray and the plane.
The example code is a little bit long. What it does:
cv::findChessboardCorners (image used is left04.jpg)cv::solvePnPCode:
#include <iostream>
#include <opencv2/opencv.hpp>
//@ref: http://answers.opencv.org/question/67008/can-i-get-2d-world-coordinates-from-a-single-image-uv-coords/
enum Pattern { CHESSBOARD, CIRCLES_GRID, ASYMMETRIC_CIRCLES_GRID };
static void calcChessboardCorners(cv::Size boardSize, float squareSize, std::vector<cv::Point3f>& corners, Pattern patternType = CHESSBOARD) {
corners.resize(0);
switch(patternType) {
case CHESSBOARD:
case CIRCLES_GRID:
for( int i = 0; i < boardSize.height; i++ )
for( int j = 0; j < boardSize.width; j++ )
corners.push_back(cv::Point3f(float(j*squareSize),
float(i*squareSize), 0));
break;
case ASYMMETRIC_CIRCLES_GRID:
for( int i = 0; i < boardSize.height; i++ )
for( int j = 0; j < boardSize.width; j++ )
corners.push_back(cv::Point3f(float((2*j + i % 2)*squareSize),
float(i*squareSize), 0));
break;
default:
CV_Error(cv::Error::StsBadArg, "Unknown pattern type\n");
}
}
double checkCameraPose(const std::vector<cv::Point3f> &modelPts, const std::vector<cv::Point2f> &imagePts, const cv::Mat &cameraMatrix,
const cv::Mat &distCoeffs, const cv::Mat &rvec, const cv::Mat &tvec) {
std::vector<cv::Point2f> projectedPts;
cv::projectPoints(modelPts, rvec, tvec, cameraMatrix, distCoeffs, projectedPts);
double rms = 0.0;
for (size_t i = 0; i < projectedPts.size(); i++) {
rms += (projectedPts[i].x-imagePts[i].x)*(projectedPts[i].x-imagePts[i].x) + (projectedPts[i].y-imagePts[i].y)*(projectedPts[i].y-imagePts[i].y);
}
return sqrt(rms / projectedPts.size());
}
cv::Point3f transformPoint(const cv::Point3f &pt, const cv::Mat &rvec, const cv::Mat &tvec) {
//Compute res = (R | T) . pt
cv::Mat rotationMatrix;
cv::Rodrigues(rvec, rotationMatrix);
cv::Mat transformationMatrix = (cv::Mat_<double>(4, 4) << rotationMatrix.at<double>(0,0), rotationMatrix.at<double>(0,1), rotationMatrix.at<double>(0,2), tvec.at<double>(0),
rotationMatrix.at<double>(1,0), rotationMatrix.at<double>(1,1), rotationMatrix.at<double>(1,2), tvec.at<double>(1),
rotationMatrix.at<double>(2,0), rotationMatrix.at<double>(2,1), rotationMatrix.at<double>(2,2), tvec.at<double>(2),
0, 0, 0, 1);
cv::Mat homogeneousPt = (cv::Mat_<double>(4, 1) << pt.x, pt.y, pt.z, 1.0);
cv::Mat transformedPtMat = transformationMatrix * homogeneousPt;
cv::Point3f transformedPt(transformedPtMat.at<double>(0), transformedPtMat.at<double>(1), transformedPtMat.at<double>(2));
return transformedPt;
}
cv::Point3f transformPointInverse(const cv::Point3f &pt, const cv::Mat &rvec, const cv::Mat &tvec) {
//Compute res = (R^t | -R^t . T) . pt
cv::Mat rotationMatrix;
cv::Rodrigues(rvec, rotationMatrix);
rotationMatrix = rotationMatrix.t();
cv::Mat translation = -rotationMatrix*tvec;
cv::Mat transformationMatrix = (cv::Mat_<double>(4, 4) << rotationMatrix.at<double>(0,0), rotationMatrix.at<double>(0,1), rotationMatrix.at<double>(0,2), translation.at<double>(0),
rotationMatrix.at<double>(1,0), rotationMatrix.at<double>(1,1), rotationMatrix.at<double>(1,2), translation.at<double>(1),
rotationMatrix.at<double>(2,0), rotationMatrix.at<double>(2,1), rotationMatrix.at<double>(2,2), translation.at<double>(2),
0, 0, 0, 1);
cv::Mat homogeneousPt = (cv::Mat_<double>(4, 1) << pt.x, pt.y, pt.z, 1.0);
cv::Mat transformedPtMat = transformationMatrix * homogeneousPt;
cv::Point3f transformedPt(transformedPtMat.at<double>(0), transformedPtMat.at<double>(1), transformedPtMat.at<double>(2));
return transformedPt;
}
void computePlaneEquation(const cv::Point3f &p0, const cv::Point3f &p1, const cv::Point3f &p2, float &a, float &b, float &c, float &d) {
//Vector p0_p1
cv::Point3f p0_p1;
p0_p1.x = p0.x - p1.x;
p0_p1.y = p0.y - p1.y;
p0_p1.z = p0.z - p1.z;
//Vector p0_p2
cv::Point3f p0_p2;
p0_p2.x = p0.x - p2.x;
p0_p2.y = p0.y - p2.y;
p0_p2.z = p0.z - p2.z;
//Normal vector
cv::Point3f n = p0_p1.cross(p0_p2);
a = n.x;
b = n.y;
c = n.z;
d = -(a*p0.x + b*p0.y + c*p0.z);
float norm = sqrt(a*a + b*b + c*c);
a /= norm;
b /= norm;
c /= norm;
d /= norm;
}
cv::Point3f compute3DOnPlaneFrom2D(const cv::Point2f &imagePt, const cv::Mat &cameraMatrix, const float a, const float b, const float c, const float d) {
double fx = cameraMatrix.at<double>(0,0);
double fy = cameraMatrix.at<double>(1,1);
double cx = cameraMatrix.at<double>(0,2);
double cy = cameraMatrix.at<double>(1,2);
cv::Point2f normalizedImagePt;
normalizedImagePt.x = (imagePt.x - cx) / fx;
normalizedImagePt.y = (imagePt.y - cy) / fy;
float s = -d / (a*normalizedImagePt.x + b*normalizedImagePt.y + c);
cv::Point3f pt;
pt.x = s*normalizedImagePt.x;
pt.y = s*normalizedImagePt.y;
pt.z = s;
return pt;
}
int main() {
cv::Mat img = cv::imread("data/left04.jpg", cv::IMREAD_GRAYSCALE);
cv::Mat view;
cv::cvtColor(img, view, cv::COLOR_GRAY2BGR);
cv::Size boardSize(9, 6);
std::vector<cv::Point2f> pointbuf;
bool found = cv::findChessboardCorners( img, boardSize, pointbuf, cv::CALIB_CB_ADAPTIVE_THRESH | cv::CALIB_CB_FAST_CHECK | cv::CALIB_CB_NORMALIZE_IMAGE);
if(found) {
cv::drawChessboardCorners( view, boardSize, cv::Mat(pointbuf), found );
} else {
return -1;
}
cv::imshow("Image", view);
cv::waitKey();
//Compute chessboard model points
std::vector<cv::Point3f> modelPts;
float squareSize = 1.0f;
calcChessboardCorners(boardSize, squareSize, modelPts);
//Intrinsic
cv::Mat cameraMatrix = (cv::Mat_<double>(3, 3) << 5.3590117051349637e+02, 0, 3.4227429926016583e+02,
0, 5.3590117051349637e+02, 2.3557560607943688e+02,
0, 0, 1);
cv::Mat distCoeffs = (cv::Mat_<double>(5, 1) << -2.6643160989580222e-01, -3.8505305722612772e-02, 1.7844280073183410e-03,
-2.7702634246810361e-04, 2.3850218962079497e-01);
//Compute camera pose
cv::Mat rvec, tvec;
cv::solvePnP(modelPts, pointbuf, cameraMatrix, distCoeffs, rvec, tvec);
//Check camera pose
double rms = checkCameraPose(modelPts, pointbuf, cameraMatrix, distCoeffs, rvec, tvec);
std::cout << "RMS error for camera pose=" << rms << std::endl;
//Transform model point (in object frame) to the camera frame
cv::Point3f pt0 = transformPoint(modelPts[0], rvec, tvec);
cv::Point3f pt1 = transformPoint(modelPts[8], rvec, tvec);
cv::Point3f pt2 = transformPoint(modelPts[53], rvec, tvec);
//Compute plane equation in the camera frame
float a, b, c, d;
computePlaneEquation(pt0, pt1, pt2, a, b, c, d);
std::cout << "Plane equation=" << a << " ; " << b << " ; " << c << " ; " << d << std::endl;
//Compute 3D from 2D
std::vector<cv::Point3f> pts3dCameraFrame, pts3dObjectFrame;
double rms_3D = 0.0;
for (size_t i = 0; i < pointbuf.size(); i++) {
cv::Point3f pt = compute3DOnPlaneFrom2D(pointbuf[i], cameraMatrix, a, b, c, d);
pts3dCameraFrame.push_back(pt);
cv::Point3f ptObjectFrame = transformPointInverse(pt, rvec, tvec);
pts3dObjectFrame.push_back(ptObjectFrame);
rms_3D += (modelPts[i].x-ptObjectFrame.x)*(modelPts[i].x-ptObjectFrame.x) + (modelPts[i].y-ptObjectFrame.y)*(modelPts[i].y-ptObjectFrame.y) +
(modelPts[i].z-ptObjectFrame.z)*(modelPts[i].z-ptObjectFrame.z);
std::cout << "modelPts[" << i << "]=" << modelPts[i] << " ; calc=" << ptObjectFrame << std::endl;
}
std::cout << "RMS error for model points=" << sqrt(rms_3D / pointbuf.size()) << std::endl;
return 0;
}