This forum is disabled, please visit https://forum.opencv.org
 | 1 | initial version |
The function solvePnP will return the rotation and translation vectors such as we have:
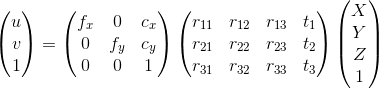
[X Y Z] are the 3D coordinates in the object frame and [u v] the 2D coordinates in the image frame.
So rvec (see Rodrigues to transform a rotation vector to a rotation matrix and vice versa) and tvec are the rotation and translation vectors that express the camera pose. With these information, you can pass from an object frame coordinate to a camera frame coordinate.
Another thing is that the when we change the coordinate from one frame to another frame, the rotation operation operates first. That means the translation vector operates in the camera frame in our case.
You should draw the different frames to get a better view of the problem.
 | 2 | No.2 Revision |
The function solvePnP will return the rotation and translation vectors such as we have:
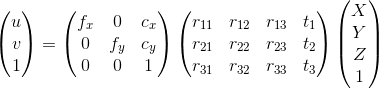
[X Y Z] are the 3D coordinates in the object frame and [u v] the 2D coordinates in the image frame.
So rvec (see Rodrigues to transform a rotation vector to a rotation matrix and vice versa) and tvec are the rotation and translation vectors that express the camera pose. With these information, you can pass from an object frame coordinate to a camera frame coordinate.
Another thing is that the when we change the coordinate from one frame to another frame, the rotation operation operates first. That means the translation vector operates in the camera frame in our case.
You should draw the different frames to get a better view of the problem.
More information on transformation matrices here (in 2D, in 3D).