Revision history [back]

I answer to the post of @Nepolo:

UPDATE 2015.07.06 -----UPDATE 2015.07.06------- UPDATE 2015.07.06

Let alpha, beta and gamma the yaw, pitch and roll angles as defined here (slide 50, Bernard BAYLE), also called Tait-Bryan angles Z1Y2X3:

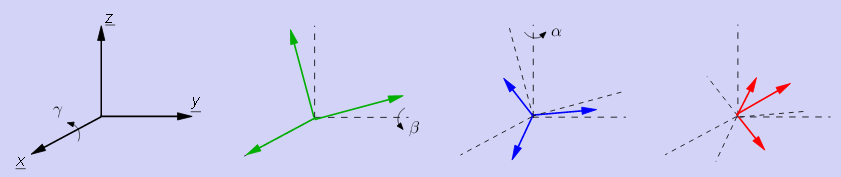
The final rotation matrix can be calculated as the the matrix resulting of the multiplication of the 3 rotations matrices about each axis:

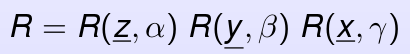
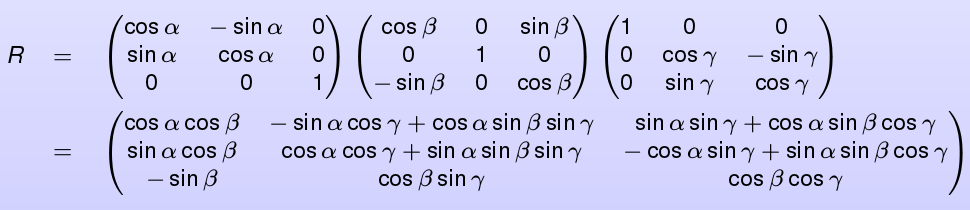
Your resulting rotation matrix is decomposed as:

  cout <<  Qx.t()<<endl;
  //RESULT
  //[1, 0, 0;
  // 0, 0.9999999980133975, 6.303336619882133e-05;
  // 0, -6.303336619882133e-05, 0.9999999980133975]


  cout <<  Qy.t()<<endl;
  //RESULT
  //[0.9999999997416501, 0, 2.273102883446428e-05;
  //0, 1, 0;
  //-2.273102883446428e-05, 0, 0.9999999997416501]


  cout <<  Qz.t()<<endl;
  //RESULT
  //[0.985944918764345, -0.1670706951047037, 0;
  //0.1670706951047037, 0.985944918764345, 0;
  //0, 0, 1]

We have Qx == identity, Qy == identity and alpha_angle=atan2(0.1670706951047037, 0.985944918764345) but you cannot end up with:

That should be the correct values Roll 5° Pitch 0° Yaw -45°

I answer to the post of @Nepolo:

UPDATE 2015.07.06 -----UPDATE 2015.07.06------- UPDATE 2015.07.06

Let alpha, beta and gamma the yaw, pitch and roll angles as defined here (slide 50, Bernard BAYLE), also called Tait-Bryan angles Z1Y2X3:

The final rotation matrix can be calculated as the the matrix resulting of the multiplication of the 3 rotations rotation matrices about each axis:

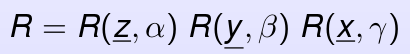
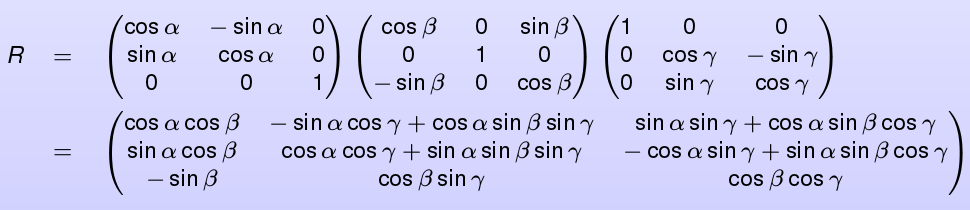
Your resulting rotation matrix is decomposed as:

  cout <<  Qx.t()<<endl;
  //RESULT
  //[1, 0, 0;
  // 0, 0.9999999980133975, 6.303336619882133e-05;
  // 0, -6.303336619882133e-05, 0.9999999980133975]


  cout <<  Qy.t()<<endl;
  //RESULT
  //[0.9999999997416501, 0, 2.273102883446428e-05;
  //0, 1, 0;
  //-2.273102883446428e-05, 0, 0.9999999997416501]


  cout <<  Qz.t()<<endl;
  //RESULT
  //[0.985944918764345, -0.1670706951047037, 0;
  //0.1670706951047037, 0.985944918764345, 0;
  //0, 0, 1]

We have Qx == identity, (more or less), Qy == identity (more or less) and alpha_angle=atan2(0.1670706951047037, 0.985944918764345) but you cannot end up with:

That should be the correct values Roll 5° Pitch 0° Yaw -45°

#include <iostream>
#include <opencv2/opencv.hpp>

cv::Mat rotationMatrixX(const double angle) {
  cv::Mat Rx = (cv::Mat_<double>(3, 3) << 1.0, 0.0, 0.0,
                                          0.0, cos(angle), -sin(angle),
                                          0.0, sin(angle), cos(angle));
  return Rx;
}

cv::Mat rotationMatrixY(const double angle) {
  cv::Mat Ry = (cv::Mat_<double>(3, 3) << cos(angle), 0.0, sin(angle),
                                          0.0, 1.0, 0.0,
                                          -sin(angle), 0.0, cos(angle));
  return Ry;
}

cv::Mat rotationMatrixZ(const double angle) {
  cv::Mat Rz = (cv::Mat_<double>(3, 3) << cos(angle), -sin(angle), 0.0,
                                          sin(angle), cos(angle), 0.0,
                                          0.0, 0.0, 1.0);
  return Rz;
}

cv::Mat yawPitchRollToRotationMatrix(const double roll, const double pitch, const double yaw) {
  cv::Mat Rx = rotationMatrixX(roll);
  cv::Mat Ry = rotationMatrixY(pitch);
  cv::Mat Rz = rotationMatrixZ(yaw);

  return Rz*Ry*Rx;
}

double rad2deg(const double rad) {
  return rad*180.0/CV_PI;
}

double deg2rad(const double deg) {
  return deg*CV_PI/180.0;
}

int main(int argc, char **argv) {
  double roll = deg2rad(5.0);
  double pitch = deg2rad(0.0);
  double yaw = deg2rad(-45.0);

  cv::Mat R = yawPitchRollToRotationMatrix(roll, pitch, yaw);
  std::cout << "R=" << R << std::endl;

  cv::Mat mtxR,mtxQ;
  cv::Mat Qx,Qy,Qz;
  cv::Vec3d e;

  e= RQDecomp3x3(R, mtxR,mtxQ,Qx, Qy, Qz);
  std::cout << "Euler angles (Roll-Pitch yaw angles) in degree=" << e << std::endl;

  return 0;
}

R=[0.7071067811865476, 0.7044160264027586, -0.06162841671621935;
  -0.7071067811865475, 0.7044160264027587, -0.06162841671621935;
  0, 0.08715574274765817, 0.9961946980917455]
Euler angles (Roll-Pitch-Yaw angles) in degree=[5, 0, -45]