This forum is disabled, please visit https://forum.opencv.org
 | 1 | initial version |
I found a solution which worked well for me. Hough transform, and the variant described above, was useful for finding the number of overlapping circles and their approximate centers, but significant optimization was required afterwards for finding the exact sizes. I also found that it was difficult to find parameter settings which worked well for all scales (in particular small circles partly overlapping large ones). Instead I did like this:
1) Get the outer contours for each connected component 2) Get the convex hull for the contour 3) Calculate the distance to the hull for each point in the contour 4) Local maxima in the distances correspond to intersection points between the circles. Split the contour at these points and fit a circle to each segment
I found this to be an easier and faster solution, but most importantly it seems to be much more robust. It typically finds all relevant circles, but there is a risk of duplicates which should be filtered out afterwards.
 | 2 | Added images |
I found a solution which worked well for me. Hough transform, and the variant described above, was useful for finding the number of overlapping circles and their approximate centers, but significant optimization was required afterwards for finding the exact sizes. I also found that it was difficult to find parameter settings which worked well for all scales (in particular small circles partly overlapping large ones). Instead I did like this:
1) Get the outer contours for each connected component 2) Get the convex hull for the contour 3) Calculate the distance to the hull for each point in the contour 4) Local maxima in the distances correspond to intersection points between the circles. Split the contour at these points and fit a circle to each segment
I found this to be an easier and faster solution, but most importantly it seems to be much more robust. It typically finds all relevant circles, but there is a risk of duplicates which should be filtered out afterwards.
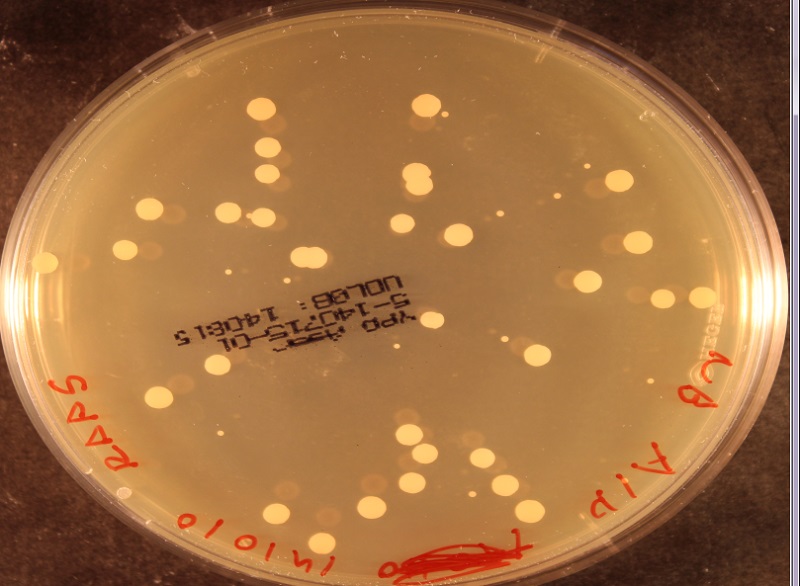
Here's an example:
Original
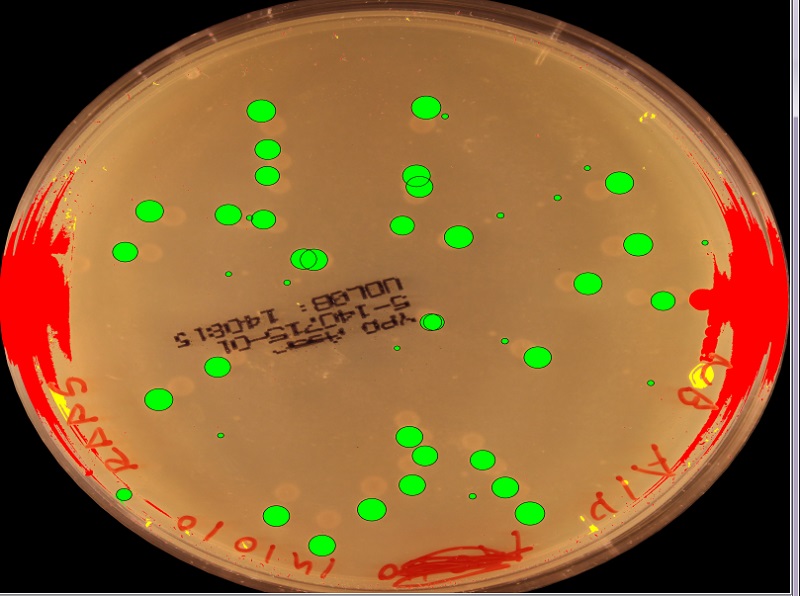
After circle detection (green objects with black fitted circles)
 | 3 | No.3 Revision |
I found came up with a solution which worked well for me. Hough transform, and the variant described above, was useful for finding the number of overlapping circles and their approximate centers, but significant optimization was required afterwards for finding the exact sizes. I also found that it was difficult to find parameter settings which worked well for all scales (in particular small circles partly overlapping large ones). Instead I did like this:
1) Get the outer contours for each connected component 2) Get the convex hull for the contour 3) Calculate the distance to the hull for each point in the contour 4) Local maxima in the distances correspond to intersection points between the circles. Split the contour at these points and fit a circle to each segment
I found this to be an easier and faster solution, but most importantly it seems to be much more robust. It typically finds all relevant circles, but there is a risk of duplicates which should be filtered out afterwards.
Here's an example:
Original

After circle detection (green objects with black fitted circles)
