Revision history [back]

What are R1 and T2?

You are extracting the camera's extrinsic parameters from the essential matrix (homography between two calibrated camera planes). The first camera is assumed to be fixed at [I|0] and the solution to the second camera is fourfold ambiguous: [R1|T1] or [R1|T2] or [R2|T1] or [R2|T2]. You can identify the correct solution by triangulating a matching pair of 2D image points. In only one of the four solutions the triangulated 3D point will be in front of both camera planes. This is explained in detail in chapter 9.6.2 of Szeliski's book.

It would be interesting to know where you got the code from, because I am currently trying to find out as well how to project the points and test if they are in front of the cameras.

Note, in Szeliski's book the assumption is made that the SVD decomposes the matrix into U*diag(1,1,0)*V'. But in OpenCV the SVD decomposition gives U*diag(l1,l2,l3)*V' with the Eigenvalues. Somehow I got along with using

R1 = svd.u*diag(svd.w)*svd.vt

But I still don't know how to compute R2 (and properly compute R1)... I'd be really thrilled to hear any thoughts on this.

On a side note, W.inv() is equal to the transpose of W.

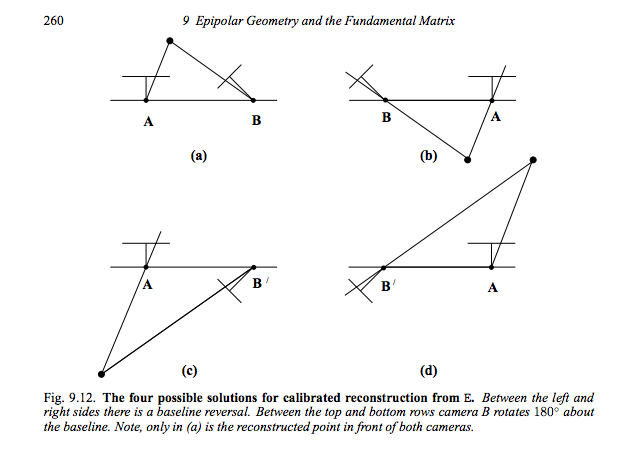
Image from Hartley, R. I. and Zisserman, A. - Multiple View Geometry in Computer Vision, 2004

What are R1 and T2?

You are extracting the camera's extrinsic parameters from the essential matrix (homography between two calibrated camera planes). The first camera is assumed to be fixed at [I|0] and the solution to the second camera is fourfold ambiguous: [R1|T1] or [R1|T2] or [R2|T1] or [R2|T2]. You can identify the correct solution by triangulating a matching pair of 2D image points. In only one of the four solutions the triangulated 3D point will be in front of both camera planes. This is explained in detail in chapter 9.6.2 of Szeliski's book.

It would be interesting to know where you got the code from, because I am currently trying to find out as well how to project the points and test if they are in front of the cameras.

Note, in Szeliski's book the assumption is made that the SVD decomposes the matrix into U*diag(1,1,0)*V'. But in OpenCV the SVD I believe, up to scale, you are good to go if the first two singular values of your decomposition gives U*diag(l1,l2,l3)*V' with the Eigenvalues. Somehow are almost equal and the third is almost zero (look into svd.w).

However, I got along with using

a related problem. My singular values are not equal at all and in summary I chose the following implementation:

static const cv::Mat W_ = (cv::Mat_<double>(3, 3) <<
                 1, 0, 0,
                 0, -1, 0,
                 0, 0, 1);
cv::Mat_<double> R1 = svd.u*diag(svd.w)*svd.vt
 
But I still don't know how to compute svd.u * diag(svd.w) * svd.vt;
cv::Mat_<double> R2 (and properly compute R1)... I'd be really thrilled to hear any thoughts on this.
 
On = svd.u * diag(svd.w) * W_ * svd.vt;
cv::Mat_<double> T1 = svd.u.col( 2 );

I am not sure about it, but maybe it helps you. I am also stuck at the point where I have to chose the correct matrix by triangulating a side note, W.inv() is equal to the transpose of W.matching point and testing whether it is in front of both cameras.

Image from Hartley, R. I. and Zisserman, A. - Multiple View Geometry in Computer Vision, 2004