This forum is disabled, please visit https://forum.opencv.org
 | 1 | initial version |
Face Recognition involves two crucial aspects: (1) extracting relevant facial features and (2) classifier design. Local Binary Patterns (LBP) have proven to yield highly discriminative features, while being computationally simple and robust against monotonic grayscale transformations. You can read up the original publication at:
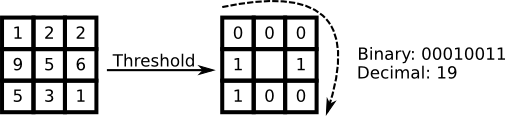
The basic idea of LBP is to summarize the local structure in an image by comparing each pixel with its neighborhood. Take a pixel as center and threshold its neighbors against. If the intensity of the center pixel is greater-equal its neighbor, then denote it with 1 and 0 if not. You'll end up with a binary number for each pixel, just like 11001111. It's easy to see, that this leads to 2^8 possible combinations, which are called Local Binary Patterns or sometimes LBP codes. The first LBP operator actually used a fixed 3 x 3 neighborhood just like this:
And here's how to calculate them with OpenCV2:
template <typename _Tp>
void OLBP_(const Mat& src, Mat& dst) {
dst = Mat::zeros(src.rows-2, src.cols-2, CV_8UC1);
for(int i=1;i<src.rows-1;i++) {
for(int j=1;j<src.cols-1;j++) {
_Tp center = src.at<_Tp>(i,j);
unsigned char code = 0;
code |= (src.at<_Tp>(i-1,j-1) > center) << 7;
code |= (src.at<_Tp>(i-1,j) > center) << 6;
code |= (src.at<_Tp>(i-1,j+1) > center) << 5;
code |= (src.at<_Tp>(i,j+1) > center) << 4;
code |= (src.at<_Tp>(i+1,j+1) > center) << 3;
code |= (src.at<_Tp>(i+1,j) > center) << 2;
code |= (src.at<_Tp>(i+1,j-1) > center) << 1;
code |= (src.at<_Tp>(i,j-1) > center) << 0;
dst.at<unsigned char>(i-1,j-1) = code;
}
}
}
For more details on the computation and LBP-variants, please see:
Now a face can now be regarded as a composition of those micro-patterns, hence we build a histogram to get the distribution. But if you throw all LBP into a single histogram all spatial information is discarded. In tasks like face detection (and a lot of other pattern recognition problems) spatial information is very useful, so it has to be incorporated into the histogram somehow. The representation proposed by Ahonen et al. in *Face Recognition with Local Binary Patterns is to divide the LBP image into grids and build a histogram of each cell seperately. Then by concatenating the histograms the spatial information is encoded (not merging them). A classification between those spatially enhanced histograms can then be performed by using a Nearest Neighbor classifier with a histogram distance, e.g. Chi-Square.
So when to choose Local Binary Patterns Histograms over Eigenfaces and Fisherfaces? Eigenfaces and Fisherfaces estimate a model based on the variance in your training data, so they perform very bad if given only few samples (you can read that up in various publications). Since a face recognition with Local Binary Patterns Histograms does not build a model explicitly, it doesn't suffer from small sample size problems.
By the way you can find an interesting LBP-variant on the face.com research page:
 | 2 | No.2 Revision |
Face Recognition involves two crucial aspects: (1) extracting relevant facial features and (2) classifier design. Local Binary Patterns (LBP) have proven to yield highly discriminative features, while being computationally simple and robust against monotonic grayscale transformations. You can read up the original publication at:
The basic idea of LBP is to summarize the local structure in an image by comparing each pixel with its neighborhood. Take a pixel as center and threshold its neighbors against. If the intensity of the center pixel is greater-equal its neighbor, then denote it with 1 and 0 if not. You'll end up with a binary number for each pixel, just like 11001111. It's easy to see, that this leads to 2^8 possible combinations, which are called Local Binary Patterns or sometimes LBP codes. The first LBP operator actually used a fixed 3 x 3 neighborhood just like this:

And here's how to calculate them with OpenCV2:
template <typename _Tp>
void OLBP_(const Mat& src, Mat& dst) {
dst = Mat::zeros(src.rows-2, src.cols-2, CV_8UC1);
for(int i=1;i<src.rows-1;i++) {
for(int j=1;j<src.cols-1;j++) {
_Tp center = src.at<_Tp>(i,j);
unsigned char code = 0;
code |= (src.at<_Tp>(i-1,j-1) > center) << 7;
code |= (src.at<_Tp>(i-1,j) > center) << 6;
code |= (src.at<_Tp>(i-1,j+1) > center) << 5;
code |= (src.at<_Tp>(i,j+1) > center) << 4;
code |= (src.at<_Tp>(i+1,j+1) > center) << 3;
code |= (src.at<_Tp>(i+1,j) > center) << 2;
code |= (src.at<_Tp>(i+1,j-1) > center) << 1;
code |= (src.at<_Tp>(i,j-1) > center) << 0;
dst.at<unsigned char>(i-1,j-1) = code;
}
}
}
For more details on the computation and LBP-variants, please see:
Now a face can now be regarded as a composition of those micro-patterns, hence we build a histogram to get the distribution. But if you throw all LBP into a single histogram all spatial information is discarded. In tasks like face detection (and a lot of other pattern recognition problems) spatial information is very useful, so it has to be incorporated into the histogram somehow. The representation proposed by Ahonen et al. in *Face Recognition with Local Binary Patterns is to divide the LBP image into grids and build a histogram of each cell seperately. Then by concatenating the histograms the spatial information is encoded (not merging them). A classification between those spatially enhanced histograms can then be performed by using a Nearest Neighbor classifier with a histogram distance, e.g. Chi-Square.
So when to choose Local Binary Patterns Histograms over Eigenfaces and Fisherfaces? Eigenfaces and Fisherfaces estimate a model based on the variance in your training data, so they perform very bad if given only few samples (you can read that up in various publications). Since a face recognition with Local Binary Patterns Histograms does not build a model explicitly, it doesn't suffer from small sample size problems.
By the way you can find an interesting LBP-variant on the face.com research page: