This forum is disabled, please visit https://forum.opencv.org
 | 1 | initial version |
I Just made some change on your code and got fine result, the rotation Mat calculation is according to your UPDATE 2.
Point p1n, p2n, p3n, p4n;
// create a new Mat with four co-ordinates
Mat co_Ordinate = (Mat_<double>(3,4) << p1.x, p2.x, p3.x, p4.x,\
p1.y, p2.y, p3.y, p4.y,\
1 , 1 , 1 , 1 );
Point2f pt(image.cols/2., image.rows/2.);
Mat r = getRotationMatrix2D(pt, -30, 1.0); // Calculate rotation Mat as in your edit
Mat rst=r*co_Ordinate; // matrix multiplication
// Access transformed co-ordinates from resultant Mat
p1n.x=(int)rst.at<double>(0,0);
p1n.y=(int)rst.at<double>(1,0);
p2n.x=(int)rst.at<double>(0,1);
p2n.y=(int)rst.at<double>(1,1);
p3n.x=(int)rst.at<double>(0,2);
p3n.y=(int)rst.at<double>(1,2);
p4n.x=(int)rst.at<double>(0,3);
p4n.y=(int)rst.at<double>(1,3);
// Draw the lines on the original image illustrating the transform
line(image, p1n, p2n, Scalar(0,0,255), 3);
line(image, p2n, p3n, Scalar(0,0,255), 3);
line(image, p3n, p4n, Scalar(0,0,255), 3);
line(image, p4n, p1n, Scalar(0,0,255), 3);
Reference:
Stackoverflow Center of rotated cv::Rect
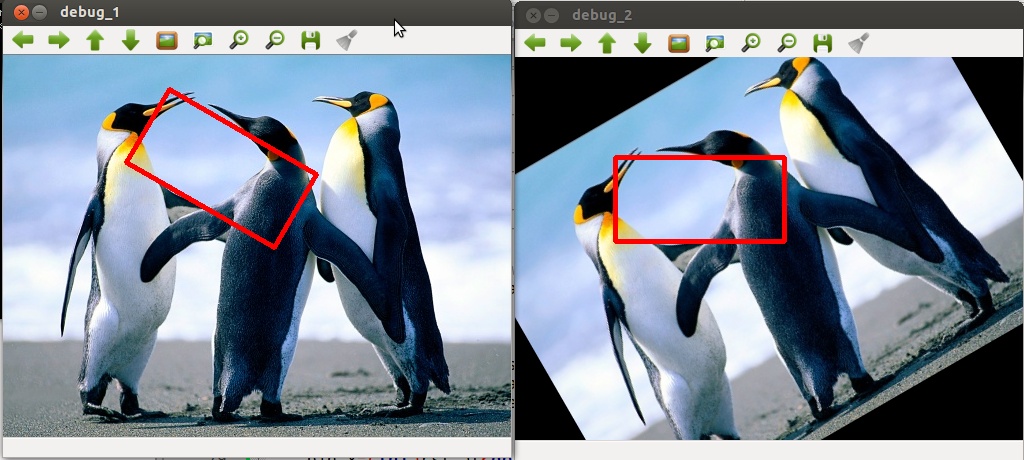
 | 2 | No.2 Revision |
I Just made some change on your code and got fine result, the rotation Mat calculation is according to your UPDATE 2.
Point p1n, p2n, p3n, p4n;
// create a new Mat with four co-ordinates
Mat co_Ordinate = (Mat_<double>(3,4) << p1.x, p2.x, p3.x, p4.x,\
p1.y, p2.y, p3.y, p4.y,\
1 , 1 , 1 , 1 );
Point2f pt(image.cols/2., image.rows/2.);
Mat r = getRotationMatrix2D(pt, -30, 1.0); // Calculate rotation Mat as in your edit
Mat rst=r*co_Ordinate; // matrix multiplication
// Access transformed co-ordinates from resultant Mat
p1n.x=(int)rst.at<double>(0,0);
p1n.y=(int)rst.at<double>(1,0);
p2n.x=(int)rst.at<double>(0,1);
p2n.y=(int)rst.at<double>(1,1);
p3n.x=(int)rst.at<double>(0,2);
p3n.y=(int)rst.at<double>(1,2);
p4n.x=(int)rst.at<double>(0,3);
p4n.y=(int)rst.at<double>(1,3);
// Draw the lines on the original image illustrating the transform
line(image, p1n, p2n, Scalar(0,0,255), 3);
line(image, p2n, p3n, Scalar(0,0,255), 3);
line(image, p3n, p4n, Scalar(0,0,255), 3);
line(image, p4n, p1n, Scalar(0,0,255), 3);
Reference:
Stackoverflow Center of rotated cv::Rect

 | 3 | No.3 Revision |
I Just made some change on your code and got fine result, the rotation Mat calculation is according to your UPDATE 2.
Point p1n, p2n, p3n, p4n;
// create a new Mat with four co-ordinates
Mat co_Ordinate = (Mat_<double>(3,4) << p1.x, p2.x, p3.x, p4.x,\
p1.y, p2.y, p3.y, p4.y,\
1 , 1 , 1 , 1 );
Point2f pt(image.cols/2., image.rows/2.);
Mat r = getRotationMatrix2D(pt, -30, 1.0); // Calculate rotation Mat as in your edit
Mat rst=r*co_Ordinate; // matrix multiplication
// Access transformed co-ordinates from resultant Mat
p1n.x=(int)rst.at<double>(0,0);
p1n.y=(int)rst.at<double>(1,0);
p2n.x=(int)rst.at<double>(0,1);
p2n.y=(int)rst.at<double>(1,1);
p3n.x=(int)rst.at<double>(0,2);
p3n.y=(int)rst.at<double>(1,2);
p4n.x=(int)rst.at<double>(0,3);
p4n.y=(int)rst.at<double>(1,3);
// Draw the lines on the original image illustrating the transform
line(image, p1n, p2n, Scalar(0,0,255), 3);
line(image, p2n, p3n, Scalar(0,0,255), 3);
line(image, p3n, p4n, Scalar(0,0,255), 3);
line(image, p4n, p1n, Scalar(0,0,255), 3);
Reference:
Stackoverflow Center of rotated cv::Rect
Image:

 | 4 | No.4 Revision |
I Just made some change on your code and got fine result, the rotation Mat calculation is according to your UPDATE 2.
Update:
According to documentation the function warpAffine transforms the source image using the specified matrix M by the equation
dst(x,y)=src(M11x+M12y+M13, M21x+M22y+M23)
So, you can translate any point in your source Mat to rotated Mat by multiplying with the corresponding Rotation matrix.
[Transposed Co-ordinates ] = [Rotation Mat] * [ SRC Co-ordinate ] | _X1 _X2 _X3 _X4 | | M11 M12 M13 | | X1 X2 X3 X4 | | | = | | * | Y1 Y2 Y3 Y4 | | _Y1 _Y2 _Y3 _Y4 | | M21 M22 M23 | | 1 1 1 1 |
The same thing you are doing in your code that is expanding the Mat and multiplication, but you are accessing rotation Mat in wrong order, that is your column and rows are interchanged. Also according to the above equation you need to add the last element of rotation Mat to corresponding co-ordinates.
So just change your code to
p1n.x = rotation_matrix.at<double>(0, 0) * p1.x + rotation_matrix.at<double>(0, 1) * p1.y+rotation_matrix.at<double>(0, 2); //here row, cols are interchanged in rotation_matrix
p1n.y = rotation_matrix.at<double>(1, 0) * p1.x + rotation_matrix.at<double>(1, 1) * p1.y+rotation_matrix.at<double>(1, 2);
p2n.x = rotation_matrix.at<double>(0, 0) * p2.x + rotation_matrix.at<double>(0, 1) * p2.y+rotation_matrix.at<double>(0, 2);
p2n.y = rotation_matrix.at<double>(1, 0) * p2.x + rotation_matrix.at<double>(1, 1) * p2.y+rotation_matrix.at<double>(1, 2);
p3n.x = rotation_matrix.at<double>(0, 0) * p3.x + rotation_matrix.at<double>(0, 1) * p3.y+rotation_matrix.at<double>(0, 2);
p3n.y = rotation_matrix.at<double>(1, 0) * p3.x + rotation_matrix.at<double>(1, 1) * p3.y+rotation_matrix.at<double>(1, 2);
p4n.x = rotation_matrix.at<double>(0, 0) * p4.x + rotation_matrix.at<double>(0, 1) * p4.y+rotation_matrix.at<double>(0, 2);
p4n.y = rotation_matrix.at<double>(1, 0) * p4.x + rotation_matrix.at<double>(1, 1) * p4.y+rotation_matrix.at<double>(1, 2);
Or you can use direct matrix multiplication as shown belwo,
Point p1n, p2n, p3n, p4n;
// create a new Mat with four co-ordinates
Mat co_Ordinate = (Mat_<double>(3,4) << p1.x, p2.x, p3.x, p4.x,\
p1.y, p2.y, p3.y, p4.y,\
1 , 1 , 1 , 1 );
Point2f pt(image.cols/2., image.rows/2.);
Mat r = getRotationMatrix2D(pt, -30, 1.0); // Calculate rotation Mat as in your edit
Mat rst=r*co_Ordinate; // matrix multiplication
// Access transformed co-ordinates from resultant Mat
p1n.x=(int)rst.at<double>(0,0);
p1n.y=(int)rst.at<double>(1,0);
p2n.x=(int)rst.at<double>(0,1);
p2n.y=(int)rst.at<double>(1,1);
p3n.x=(int)rst.at<double>(0,2);
p3n.y=(int)rst.at<double>(1,2);
p4n.x=(int)rst.at<double>(0,3);
p4n.y=(int)rst.at<double>(1,3);
// Draw the lines on the original image illustrating the transform
line(image, p1n, p2n, Scalar(0,0,255), 3);
line(image, p2n, p3n, Scalar(0,0,255), 3);
line(image, p3n, p4n, Scalar(0,0,255), 3);
line(image, p4n, p1n, Scalar(0,0,255), 3);
Reference:
Stackoverflow Center of rotated cv::Rect
Image:

 | 5 | No.5 Revision |
I Just made some change on your code and got fine result, the rotation Mat calculation is according to your UPDATE 2.
Update:
According to documentation the function warpAffine transforms the source image using the specified matrix M by the equation
dst(x,y)=src(M11x+M12y+M13, M21x+M22y+M23)
So, you can translate any point in your source Mat to rotated Mat by multiplying with the corresponding Rotation matrix.
[Transposed Co-ordinates ] = [Rotation Mat] * [ SRC Co-ordinate ] | _X1 _X2 _X3 _X4 | | M11 M12 M13 | | X1 X2 X3 X4 | | | = | | * | Y1 Y2 Y3 Y4 | | _Y1 _Y2 _Y3 _Y4 | | M21 M22 M23 | | 1 1 1 1 |
So just change your code to
p1n.x = rotation_matrix.at<double>(0, 0) * p1.x + rotation_matrix.at<double>(0, 1) * p1.y+rotation_matrix.at<double>(0, 2); //here row, cols are interchanged in rotation_matrix
p1n.y = rotation_matrix.at<double>(1, 0) * p1.x + rotation_matrix.at<double>(1, 1) * p1.y+rotation_matrix.at<double>(1, 2);
2);
p2n.x = rotation_matrix.at<double>(0, 0) * p2.x + rotation_matrix.at<double>(0, 1) * p2.y+rotation_matrix.at<double>(0, 2);
p2n.y = rotation_matrix.at<double>(1, 0) * p2.x + rotation_matrix.at<double>(1, 1) * p2.y+rotation_matrix.at<double>(1, 2);
p3n.x = rotation_matrix.at<double>(0, 0) * p3.x + rotation_matrix.at<double>(0, 1) * p3.y+rotation_matrix.at<double>(0, 2);
p3n.y = rotation_matrix.at<double>(1, 0) * p3.x + rotation_matrix.at<double>(1, 1) * p3.y+rotation_matrix.at<double>(1, 2);
p4n.x = rotation_matrix.at<double>(0, 0) * p4.x + rotation_matrix.at<double>(0, 1) * p4.y+rotation_matrix.at<double>(0, 2);
p4n.y = rotation_matrix.at<double>(1, 0) * p4.x + rotation_matrix.at<double>(1, 1) * p4.y+rotation_matrix.at<double>(1, 2);
Or you can use direct matrix multiplication as shown belwo,
Point p1n, p2n, p3n, p4n;
// create a new Mat with four co-ordinates
Mat co_Ordinate = (Mat_<double>(3,4) << p1.x, p2.x, p3.x, p4.x,\
p1.y, p2.y, p3.y, p4.y,\
1 , 1 , 1 , 1 );
Point2f pt(image.cols/2., image.rows/2.);
Mat r = getRotationMatrix2D(pt, -30, 1.0); // Calculate rotation Mat as in your edit
Mat rst=r*co_Ordinate; // matrix multiplication
// Access transformed co-ordinates from resultant Mat
p1n.x=(int)rst.at<double>(0,0);
p1n.y=(int)rst.at<double>(1,0);
p2n.x=(int)rst.at<double>(0,1);
p2n.y=(int)rst.at<double>(1,1);
p3n.x=(int)rst.at<double>(0,2);
p3n.y=(int)rst.at<double>(1,2);
p4n.x=(int)rst.at<double>(0,3);
p4n.y=(int)rst.at<double>(1,3);
// Draw the lines on the original image illustrating the transform
line(image, p1n, p2n, Scalar(0,0,255), 3);
line(image, p2n, p3n, Scalar(0,0,255), 3);
line(image, p3n, p4n, Scalar(0,0,255), 3);
line(image, p4n, p1n, Scalar(0,0,255), 3);
Reference:
Stackoverflow Center of rotated cv::Rect
Image:

 | 6 | No.6 Revision |
I Just made some change on your code and got fine result, the rotation Mat calculation is according to your UPDATE 2.
Update:
According to documentation the function warpAffine transforms the source image using the specified matrix M by the equation
dst(x,y)=src(M11x+M12y+M13, M21x+M22y+M23)
So, you can translate any point in your source Mat to rotated Mat by multiplying with the corresponding Rotation matrix.
[Transposed Co-ordinates ] = [Rotation Mat] * [ SRC Co-ordinate ] | _X1 _X2 _X3 _X4 | | M11 M12 M13 | | X1 X2 X3 X4 | | | = | | * | Y1 Y2 Y3 Y4 | | _Y1 _Y2 _Y3 _Y4 | | M21 M22 M23 | | 1 1 1 1 |
The same thing you are doing in your code that is expanding the Mat and multiplication, but you are accessing rotation Mat in wrong order, that is your column and rows are interchanged. Also according to the above equation you need to add the last element of rotation Mat to corresponding co-ordinates, and the last thing is change caste float to double.
So just change your code to
p1n.x = rotation_matrix.at<double>(0, 0) * p1.x + rotation_matrix.at<double>(0, 1) * p1.y+rotation_matrix.at<double>(0, 2); //here row, cols are interchanged in rotation_matrix
p1n.y = rotation_matrix.at<double>(1, 0) * p1.x + rotation_matrix.at<double>(1, 1) * p1.y+rotation_matrix.at<double>(1, 2);
p2n.x = rotation_matrix.at<double>(0, 0) * p2.x + rotation_matrix.at<double>(0, 1) * p2.y+rotation_matrix.at<double>(0, 2);
p2n.y = rotation_matrix.at<double>(1, 0) * p2.x + rotation_matrix.at<double>(1, 1) * p2.y+rotation_matrix.at<double>(1, 2);
p3n.x = rotation_matrix.at<double>(0, 0) * p3.x + rotation_matrix.at<double>(0, 1) * p3.y+rotation_matrix.at<double>(0, 2);
p3n.y = rotation_matrix.at<double>(1, 0) * p3.x + rotation_matrix.at<double>(1, 1) * p3.y+rotation_matrix.at<double>(1, 2);
p4n.x = rotation_matrix.at<double>(0, 0) * p4.x + rotation_matrix.at<double>(0, 1) * p4.y+rotation_matrix.at<double>(0, 2);
p4n.y = rotation_matrix.at<double>(1, 0) * p4.x + rotation_matrix.at<double>(1, 1) * p4.y+rotation_matrix.at<double>(1, 2);
Or you can use direct matrix multiplication as shown belwo,
Point p1n, p2n, p3n, p4n;
// create a new Mat with four co-ordinates
Mat co_Ordinate = (Mat_<double>(3,4) << p1.x, p2.x, p3.x, p4.x,\
p1.y, p2.y, p3.y, p4.y,\
1 , 1 , 1 , 1 );
Point2f pt(image.cols/2., image.rows/2.);
Mat r = getRotationMatrix2D(pt, -30, 1.0); // Calculate rotation Mat as in your edit
Mat rst=r*co_Ordinate; // matrix multiplication
// Access transformed co-ordinates from resultant Mat
p1n.x=(int)rst.at<double>(0,0);
p1n.y=(int)rst.at<double>(1,0);
p2n.x=(int)rst.at<double>(0,1);
p2n.y=(int)rst.at<double>(1,1);
p3n.x=(int)rst.at<double>(0,2);
p3n.y=(int)rst.at<double>(1,2);
p4n.x=(int)rst.at<double>(0,3);
p4n.y=(int)rst.at<double>(1,3);
// Draw the lines on the original image illustrating the transform
line(image, p1n, p2n, Scalar(0,0,255), 3);
line(image, p2n, p3n, Scalar(0,0,255), 3);
line(image, p3n, p4n, Scalar(0,0,255), 3);
line(image, p4n, p1n, Scalar(0,0,255), 3);
Reference:
Stackoverflow Center of rotated cv::Rect
Image:

 | 7 | No.7 Revision |
I Just made some change on your code and got fine result, the rotation Mat calculation is according to your UPDATE 2.
Update:
According to documentation the function warpAffine transforms the source image using the specified matrix M by the equation
dst(x,y)=src(M11x+M12y+M13, M21x+M22y+M23)
So, you can translate any point in your source Mat to rotated Mat by multiplying with the corresponding Rotation matrix.
[Transposed Co-ordinates ] = [Rotation Mat] * [ SRC Co-ordinate ] | _X1 _X2 _X3 _X4 | | M11 M12 M13 | | X1 X2 X3 X4 | | | = | | * | Y1 Y2 Y3 Y4 | | _Y1 _Y2 _Y3 _Y4 | | M21 M22 M23 | | 1 1 1 1 |
So just change your code to
p1n.x = rotation_matrix.at<double>(0, 0) * p1.x + rotation_matrix.at<double>(0, 1) * p1.y+rotation_matrix.at<double>(0, 2); //here row, cols are interchanged in rotation_matrix
p1n.y = rotation_matrix.at<double>(1, 0) * p1.x + rotation_matrix.at<double>(1, 1) * p1.y+rotation_matrix.at<double>(1, 2);
p2n.x = rotation_matrix.at<double>(0, 0) * p2.x + rotation_matrix.at<double>(0, 1) * p2.y+rotation_matrix.at<double>(0, 2);
p2n.y = rotation_matrix.at<double>(1, 0) * p2.x + rotation_matrix.at<double>(1, 1) * p2.y+rotation_matrix.at<double>(1, 2);
p3n.x = rotation_matrix.at<double>(0, 0) * p3.x + rotation_matrix.at<double>(0, 1) * p3.y+rotation_matrix.at<double>(0, 2);
p3n.y = rotation_matrix.at<double>(1, 0) * p3.x + rotation_matrix.at<double>(1, 1) * p3.y+rotation_matrix.at<double>(1, 2);
p4n.x = rotation_matrix.at<double>(0, 0) * p4.x + rotation_matrix.at<double>(0, 1) * p4.y+rotation_matrix.at<double>(0, 2);
p4n.y = rotation_matrix.at<double>(1, 0) * p4.x + rotation_matrix.at<double>(1, 1) * p4.y+rotation_matrix.at<double>(1, 2);
Or you can use direct matrix multiplication as shown belwo,
Point p1n, p2n, p3n, p4n;
// create a new Mat with four co-ordinates
Mat co_Ordinate = (Mat_<double>(3,4) << p1.x, p2.x, p3.x, p4.x,\
p1.y, p2.y, p3.y, p4.y,\
1 , 1 , 1 , 1 );
Point2f pt(image.cols/2., image.rows/2.);
Mat r = getRotationMatrix2D(pt, -30, 1.0); // Calculate rotation Mat as in your edit
Mat rst=r*co_Ordinate; // matrix multiplication
// Access transformed co-ordinates from resultant Mat
p1n.x=(int)rst.at<double>(0,0);
p1n.y=(int)rst.at<double>(1,0);
p2n.x=(int)rst.at<double>(0,1);
p2n.y=(int)rst.at<double>(1,1);
p3n.x=(int)rst.at<double>(0,2);
p3n.y=(int)rst.at<double>(1,2);
p4n.x=(int)rst.at<double>(0,3);
p4n.y=(int)rst.at<double>(1,3);
// Draw the lines on the original image illustrating the transform
line(image, p1n, p2n, Scalar(0,0,255), 3);
line(image, p2n, p3n, Scalar(0,0,255), 3);
line(image, p3n, p4n, Scalar(0,0,255), 3);
line(image, p4n, p1n, Scalar(0,0,255), 3);
Image:
