This forum is disabled, please visit https://forum.opencv.org
 | 1 | initial version |
I don't think there is anything fundamentally wrong with your processing pipeline idea, this is a pretty standard approach used in monocular SLAM, which is likely why it works in some cases. I cannot say for certain from the code you have posted, as it seems that some of the syntax got corrupted, but one thing I think that is missing is the rectification (undistortion) of the individual images before performing feature detection.
Estimation of the fundamental matrix depends upon having point correspondences between both images that are undistorted (as near ideal pinhole camera as possible). Lens distortion is nonlinear and depending upon how close the matched features are to the center of projection, you will get more or less correct fundamental matrix estimates, which directly effects the quality of the stereo rectification. So to summarize I recommend performing undistortion immediately after reading in your input images.
 | 2 | No.2 Revision |
I don't think there is anything fundamentally wrong with Upon looking into your problem in more detail, the source of your rectification errors has become a bit more obvious. Your processing pipeline idea, up until the decomposition of the essential into rotation and translation is mostly correct (see comments further below). When decomposing the essential matrix into rotation and translation components, there are actually 4 possible configurations, where only one of them is actually valid for a given camera pair. Basically the decomposition is not unique because it allows degenerate configurations where one or both of the cameras are oriented away from the scene they imaged. The solution to this is a pretty standard approach used in monocular SLAM, which is likely why it works in some cases. problem is to test if an arbitrary 3D point, derived from a point pair correspondences between both images, is located in front of each camera. In only one of the four configurations will the 3D point be located in front of both cameras. Assuming the first camera is set to the identity the four cases are:
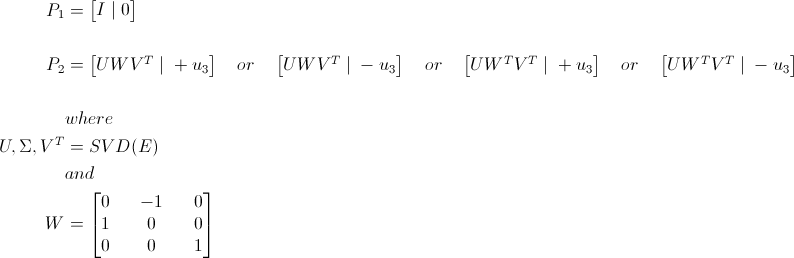
where P1 is the camera matrix for the first camera and P2 for the second.
Testing whether any given 3D point, derived from a point correspondence in both images, is in front of both cameras for one of the four possible rotation and translation combinations, is a bit more involved. This is because you initially only have the point's projection in each image but lack the point's depth. Assuming X, X' is a 3d point imaged in the first and second cameras coordinate system respectively, and (ũ,ṽ), (ũ', ṽ') the corresponding projection in normalized image coordinates, in the first and second camera images respectively, we can use a rotation translation pair to estimate the 3D points depth in each camera coordinate system:
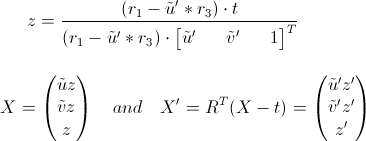
where r1 .. r3 are the rows of the rotation matrix R and translation t. Using the formula above for a point correspondence pair you can determine the associated 3D point's position in each camera coordinate system. If z or z' are negative, then you know you have a a degenerate configuration and you have to try one of the other three essential matrix decompositions. I cannot say for certain from the code you have posted, as it seems that some of the syntax got corrupted, but one thing I think that is missing is the made a gist of this in python here: https://gist.github.com/jensenb/8668000#file-decompose_essential_matrix-py
Besides this You are not performing rectification (undistortion) of the individual images before performing prior to feature detection. extraction / matching, which can cause some problems down the line, depending upon how strong the lens distortion is in your setup.
Estimation of the fundamental matrix depends upon having point correspondences between both images that are undistorted (as near ideal pinhole camera as possible). Lens distortion is nonlinear and depending upon how close the matched features are to the center of projection, you will get more or less correct fundamental matrix estimates, which directly effects the quality of the stereo rectification. So to summarize I recommend performing undistortion immediately after reading in your input images.