This forum is disabled, please visit https://forum.opencv.org
 | 1 | initial version |
My first advice is to look at a course or a book on rigid body transformation, homogeneous transformation topics. These topics are well-covered in a robotics or computer graphics course, for instance:
You have to understand what rvec and tvec are. First the camera model used in computer vision is described here. Additional information on pose estimation are described here.
rvec is a Rodrigues rotation vector, or axis-angle representation.
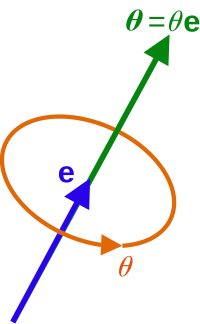
Rotation direction is described by a unit vector and the "amount" of rotation by the length of the vector. This representation avoids issues you can have with Euler angles, i.e. Gimbal lock. Quaternion is another representation of rotation that don't have Gimbal lock issue.
Now, what rvec and tvec represent?
They allow transforming a 3D point expressed in one coordinate system to another one. Here, you transform 3D points expressed in the tag frame into the camera frame:
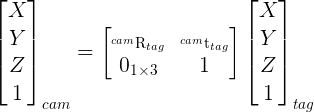
So, for the first case you should have (here I use the tag X-axis as an example):
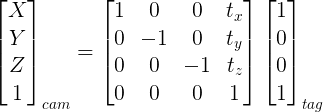
For trivial case, you can recover the rotation matrix by looking at the values that allow transforming the X-axis, Y-axis and Z-axis of the tag into the camera frame.
 | 2 | No.2 Revision |
My first advice is to look at a course or a book on rigid body transformation, homogeneous transformation topics. These topics are well-covered in a robotics or computer graphics course, for instance:
You have to understand what rvec and tvec are. First the camera model used in computer vision is described here. Additional information on pose estimation are described here.
rvec is a Rodrigues rotation vector, or axis-angle representation.

Rotation direction is described by a unit vector and the "amount" of rotation by the length of the vector. This representation avoids issues you can have with Euler angles, i.e. Gimbal lock. Quaternion is another representation of rotation that don't have Gimbal lock issue.
Most important, they are not Euler angles.
Now, what rvec and tvec represent?
They allow transforming a 3D point expressed in one coordinate system to another one. Here, you transform 3D points expressed in the tag frame into the camera frame:
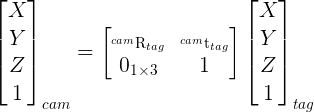
So, for the first case you should have (here I use the tag X-axis as an example):
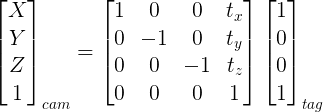
For trivial case, you can recover the rotation matrix by looking at the values that allow transforming the X-axis, Y-axis and Z-axis of the tag into the camera frame.
In my opinion, it is very rare to need to use the Euler angles and I don't like them. Why?
First, because they are 12 different representations/conventions of Euler angles. So first you have to agree on which Euler convention you are using when you have to deal with other people / code.
Then, Gimbal lock.
You only need Euler angles when you have to be able to interpret the rotation. So only for printing or as an user input (e.g. to rotate a CAD model in Blender).
Rest of the time, computation should be / are done using the rotation matrix or quaternion representations.