Revision history [back]

well, i think, you got your cubemaps in wrong order. using this convention:

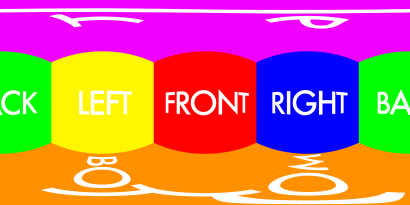
we can map cube coords to equirectangular in a straightforward way (some python code):

def get_theta_phi( _x, _y, _z):
    dv = math.sqrt(_x*_x + _y*_y + _z*_z)
    x = _x/dv
    y = _y/dv
    z = _z/dv
    theta = math.atan2(y, x)
    phi = math.asin(z)
    return theta, phi


# x,y position in cubemap
# cw  cube width
# W,H size of equirectangular image
def map_cube(x, y, side, cw, W, H):

    u = 2*(float(x)/cw - 0.5)
    v = 2*(float(y)/cw - 0.5)

    if side == "front":
        theta, phi = get_theta_phi( 1, u, v )
    elif side == "right":
        theta, phi = get_theta_phi( -u, 1, v )
    elif side == "left":
        theta, phi = get_theta_phi( u, -1, v )
    elif side == "back":
        theta, phi = get_theta_phi( -1, u, v )
    elif side == "bottom":
        theta, phi = get_theta_phi( -v, u, 1 )
    elif side == "top":
        theta, phi = get_theta_phi( v, u, -1 )

    _u = 0.5+0.5*(theta/math.pi)
    _v = 0.5+(phi/math.pi)
    return _u*W,  _v*H


print map_cube(194, 175, "right", 250, 1000, 500)

(830.2741600023378, 303.610428544235)

well, i think, you got your cubemaps in wrong order. using this convention:

we can map cube coords to equirectangular in a straightforward way (some python code):

def get_theta_phi( _x, _y, _z):
    dv = math.sqrt(_x*_x + _y*_y + _z*_z)
    x = _x/dv
    y = _y/dv
    z = _z/dv
    theta = math.atan2(y, x)
    phi = math.asin(z)
    return theta, phi


# x,y position in cubemap
# cw  cube width
# W,H size of equirectangular image
def map_cube(x, y, side, cw, W, H):

    u = 2*(float(x)/cw - 0.5)
    v = 2*(float(y)/cw - 0.5)

    if side == "front":
        theta, phi = get_theta_phi( 1, u, v )
    elif side == "right":
        theta, phi = get_theta_phi( -u, 1, v )
    elif side == "left":
        theta, phi = get_theta_phi( u, -1, v )
    elif side == "back":
        theta, phi = get_theta_phi( -1, u, -u, v )
    elif side == "bottom":
        theta, phi = get_theta_phi( -v, u, 1 )
    elif side == "top":
        theta, phi = get_theta_phi( v, u, -1 )

    _u = 0.5+0.5*(theta/math.pi)
    _v = 0.5+(phi/math.pi)
    return _u*W,  _v*H


print map_cube(194, 175, "right", 250, 1000, 500)

(830.2741600023378, 303.610428544235)