This forum is disabled, please visit https://forum.opencv.org
 | 1 | initial version |
I think i acted too fast. I took a closer look now and compared my results with the one of Matlab once again. I know the matrizes of matlab are not normalized. So i think they are not compareable. However i dont get your results either.
Matlab Results:
S1: 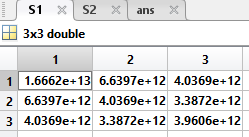
S2: 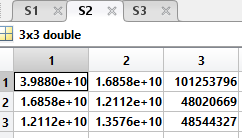
S3: 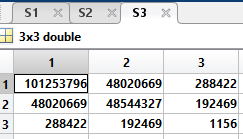
T: 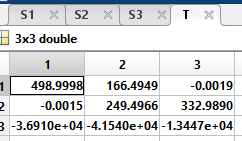
S2*T: 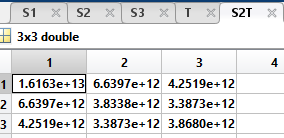
M: 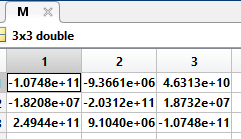
New C++ Code:
float LeastSquaresEllipseFit(unsigned int *xCors, unsigned int *yCors,
unsigned int startID, unsigned int stopID){
unsigned int length = (stopID - startID) + 1;
double mx = 0, my = 0;
cv::Mat XY(length, 2, CV_64F);
cv::Mat D1(length, 3, CV_64F);
cv::Mat D2(length, 3, CV_64F);
cv::Mat S1(3, 3, CV_64F);
cv::Mat S2(3, 3, CV_64F);
cv::Mat S3(3, 3, CV_64F);
for (unsigned int i = 0; i < length; i++)
{
mx += xCors[i];
my += yCors[i];
}
mx /= length;
my /= length;
if (mx != 0 && my!= 0)
for (unsigned int i = 0; i < length; i++)
{
XY.at<double>(i, 0) = (xCors[i] - mx) / mx;
XY.at<double>(i, 1) = (yCors[i] - my) / my;
}
//Compute design matrix
for (unsigned int i = 0; i < length; i++)
{
D1.at<double>(i, 0) = XY.at<double>(i, 0) * XY.at<double>(i, 0); //x²
D1.at<double>(i, 1) = XY.at<double>(i, 0) * XY.at<double>(i, 1); //xy
D1.at<double>(i, 2) = XY.at<double>(i, 1) * XY.at<double>(i, 1); //y²
D2.at<double>(i, 0) = XY.at<double>(i, 0); //x
D2.at<double>(i, 1) = XY.at<double>(i, 1); //y
D2.at<double>(i, 2) = 1;
}
cv::Mat T(3, 3, CV_64F);
cv::Mat M(3, 3, CV_64F);
cv::Mat C(3, 3, CV_64F);
cv::Mat EVal, EVec;
//Fill constraint matrix
C.setTo(0);
C.at<double>(0, 2) = 2;
C.at<double>(1, 1) = -1;
C.at<double>(2, 0) = 2;
//Solve Ax² + Bxy + Cy² + Dx + Ey + F = 0
S1 = D1.t() * D1;
S2 = D1.t() * D2;
S3 = D2.t() * D2;
T = -S3.inv(cv::DECOMP_SVD) * S2.t();
M = C.inv() * (S1 + S2*(T));
cv::eigen(M, EVal, EVec);
//Condition: 4ac - b² > 0
cv::Mat cond = 4 * EVec.row(0).mul(EVec.row(2)) - EVec.row(1).mul(EVec.row(1));
#ifdef DEBUG
cout << "S1: " << S1 << endl;
cout << "S2: " << S2 << endl;
cout << "S3: " << S2 << endl;
cout << "T: " << T << endl;
cout << "S2 * T: " << S2 * T << endl;
cout << "M" << M << endl;
cout << "Eigenvalue: " << EVal << endl;
cout << "Eigenvector: " << EVec << endl;
cout << "Condition: " << cond << endl;
#endif
//Find eigenvalue based on condition
unsigned int index;
for (unsigned int i = 0; i < cond.cols; i++)
{
if (cond.at<double>(i) > 0)
index = i;
}
cv::Mat abc = EVec.col(index);
cv::Mat def = T * EVec.col(index);
double a = abc.at<double>(0, 0);
double b = abc.at<double>(1, 0);
double c = abc.at<double>(2, 0);
double d = def.at<double>(0, 0);
double e = def.at<double>(1, 0);
double f = def.at<double>(2, 0);
#ifdef DEBUG
cout << "[a b c] =" << abc << endl;
cout << "[d e f] =" << def << endl;
#endif
//http://math.stackexchange.com/questions/616645/determining-the-major-minor-axes-of-an-ellipse-from-general-form
//Coefficent normalizing factor
double q = (64 * f*(4 * a*c - b*b) - 64 * (a*e*e - b*d*e - c*d*d)) / ((4 * a*c - b*b)*(4 * a*c - b*b));
//Distance between center and focal point
double s = (1 / 4) * sqrt(abs(q)*sqrt(b*b + (a - c)*(a - c)));
double rmax = (1/8)*sqrt(2 * abs(q)*sqrt(b*b + (a - c)*(a - c)) - 2 * q*(a + c));
double rmin = sqrt(rmax*rmax - s *s);
double cx = (b * e - 2 * c * d) / (4 * a * c - b * b);
double cy = (b * d - 2 * a * e) / (4 * a * c - b * b);
//Placeholder atm
float coef = 123;
return abs(coef);
C++ Results:
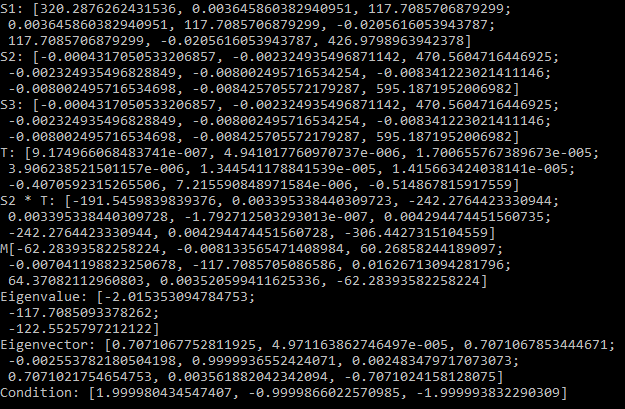
 | 2 | No.2 Revision |
EDIT: I think i acted too fast. I took a closer look now and compared my results with the one of Matlab once again. I know the matrizes of matlab are not normalized. So i think they are not compareable. However i dont get your results either.
Matlab Results:
S1: 
S2: 
S3: 
T: 
S2*T: 
M: 
New C++ Code:
float LeastSquaresEllipseFit(unsigned int *xCors, unsigned int *yCors,
unsigned int startID, unsigned int stopID){
unsigned int length = (stopID - startID) + 1;
double mx = 0, my = 0;
cv::Mat XY(length, 2, CV_64F);
cv::Mat D1(length, 3, CV_64F);
cv::Mat D2(length, 3, CV_64F);
cv::Mat S1(3, 3, CV_64F);
cv::Mat S2(3, 3, CV_64F);
cv::Mat S3(3, 3, CV_64F);
for (unsigned int i = 0; i < length; i++)
{
mx += xCors[i];
my += yCors[i];
}
mx /= length;
my /= length;
if (mx != 0 && my!= 0)
for (unsigned int i = 0; i < length; i++)
{
XY.at<double>(i, 0) = (xCors[i] - mx) / mx;
XY.at<double>(i, 1) = (yCors[i] - my) / my;
}
//Compute design matrix
for (unsigned int i = 0; i < length; i++)
{
D1.at<double>(i, 0) = XY.at<double>(i, 0) * XY.at<double>(i, 0); //x²
D1.at<double>(i, 1) = XY.at<double>(i, 0) * XY.at<double>(i, 1); //xy
D1.at<double>(i, 2) = XY.at<double>(i, 1) * XY.at<double>(i, 1); //y²
D2.at<double>(i, 0) = XY.at<double>(i, 0); //x
D2.at<double>(i, 1) = XY.at<double>(i, 1); //y
D2.at<double>(i, 2) = 1;
}
cv::Mat T(3, 3, CV_64F);
cv::Mat M(3, 3, CV_64F);
cv::Mat C(3, 3, CV_64F);
cv::Mat EVal, EVec;
//Fill constraint matrix
C.setTo(0);
C.at<double>(0, 2) = 2;
C.at<double>(1, 1) = -1;
C.at<double>(2, 0) = 2;
//Solve Ax² + Bxy + Cy² + Dx + Ey + F = 0
S1 = D1.t() * D1;
S2 = D1.t() * D2;
S3 = D2.t() * D2;
T = -S3.inv(cv::DECOMP_SVD) * S2.t();
M = C.inv() * (S1 + S2*(T));
cv::eigen(M, EVal, EVec);
//Condition: 4ac - b² > 0
cv::Mat cond = 4 * EVec.row(0).mul(EVec.row(2)) - EVec.row(1).mul(EVec.row(1));
#ifdef DEBUG
cout << "S1: " << S1 << endl;
cout << "S2: " << S2 << endl;
cout << "S3: " << S2 << endl;
cout << "T: " << T << endl;
cout << "S2 * T: " << S2 * T << endl;
cout << "M" << M << endl;
cout << "Eigenvalue: " << EVal << endl;
cout << "Eigenvector: " << EVec << endl;
cout << "Condition: " << cond << endl;
#endif
//Find eigenvalue based on condition
unsigned int index;
for (unsigned int i = 0; i < cond.cols; i++)
{
if (cond.at<double>(i) > 0)
index = i;
}
cv::Mat abc = EVec.col(index);
cv::Mat def = T * EVec.col(index);
double a = abc.at<double>(0, 0);
double b = abc.at<double>(1, 0);
double c = abc.at<double>(2, 0);
double d = def.at<double>(0, 0);
double e = def.at<double>(1, 0);
double f = def.at<double>(2, 0);
#ifdef DEBUG
cout << "[a b c] =" << abc << endl;
cout << "[d e f] =" << def << endl;
#endif
//http://math.stackexchange.com/questions/616645/determining-the-major-minor-axes-of-an-ellipse-from-general-form
//Coefficent normalizing factor
double q = (64 * f*(4 * a*c - b*b) - 64 * (a*e*e - b*d*e - c*d*d)) / ((4 * a*c - b*b)*(4 * a*c - b*b));
//Distance between center and focal point
double s = (1 / 4) * sqrt(abs(q)*sqrt(b*b + (a - c)*(a - c)));
double rmax = (1/8)*sqrt(2 * abs(q)*sqrt(b*b + (a - c)*(a - c)) - 2 * q*(a + c));
double rmin = sqrt(rmax*rmax - s *s);
double cx = (b * e - 2 * c * d) / (4 * a * c - b * b);
double cy = (b * d - 2 * a * e) / (4 * a * c - b * b);
//Placeholder atm
float coef = 123;
return abs(coef);
C++ Results:
