Why degree from image is not the same at the theory in math?
Hello, I have question on the degree calculated from the atan function between two points (x1,y1) and (x2,y2). From what I get from the online tutorial, the formula would be atan((y2-y1)/(x2-x1)) and convert it to degree later. Please refer to the image below.C:\fakepath\degree.png
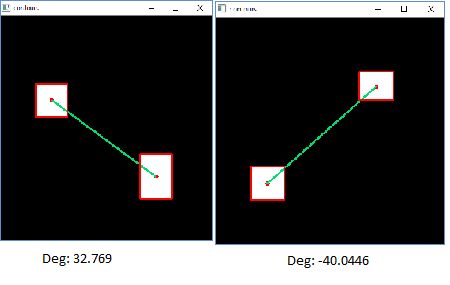
The question is, if there is negative degree value, in normal mathematical quadrant, it will be located in quadrant 2 and 4 but from the picture it shows that it is in quadrant 1 and 3. Am I correct in interpreting this degree in terms of image processing?
